Fisher consistency of supervised learning methods
Fabian Pedregosa
Chaire Havas-Dauphine Economie des nouvelles données/CEREMADE CNRS-UMR 7534

Outline
- 1. Binary class classification.
- Bartlett, P. L., Jordan, M. I., & McAuliffe, J. D. (2003). Convexity , Classification , and Risk Bounds. Journal of the American Statistical Association.
- 2. Ordinal regression.
- Pedregosa, F., Bach, F., Gramfort, A., On the Consistency of Ordinal Regression Methods. ArXiv 2015
- 3. Ranking.
- Duchi, J. C., Mackey, L. W., & Jordan, M. I. (2010). On the Consistency of Ranking Algorithms. ICML 2010
- 4. Open problem.
Binary class problem
Given $n$ training pairs $\{(X_1, y_1), \ldots, (X_n, y_n)\}$, $X_i \in \RR^2, y_i \in \{-1, +1\}$
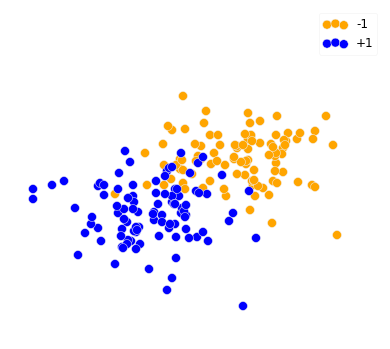
Learn a hyperplane $w \in \mathbb{R}^2$ such that it separates both classes: $\text{sign}(w^T X_i) = y_i$
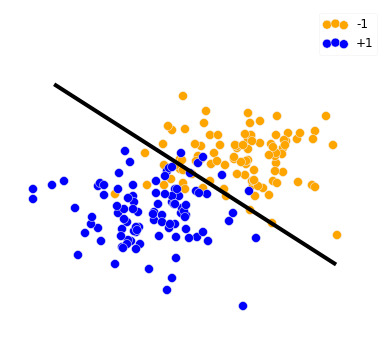
Binary class problem

A decision function that separates both classes might not exist.
The next best thing $\implies$ minimize number of samples where $\text{sign}(w^T X_i) \neq y_i \iff y_i w^T X_i \lt 0$
$$\text{argmin}_w \frac{1}{n} \sum_{i=1}^n \ell(y_i w^T X_i)$$
where $\ell(t)$ =
Binary class problem
$$\text{argmin}_{w \in \RR^2} \frac{1}{n} \sum_{i=1}^n \ell(y_i w^T X_i)$$
Minimization of the cost function: 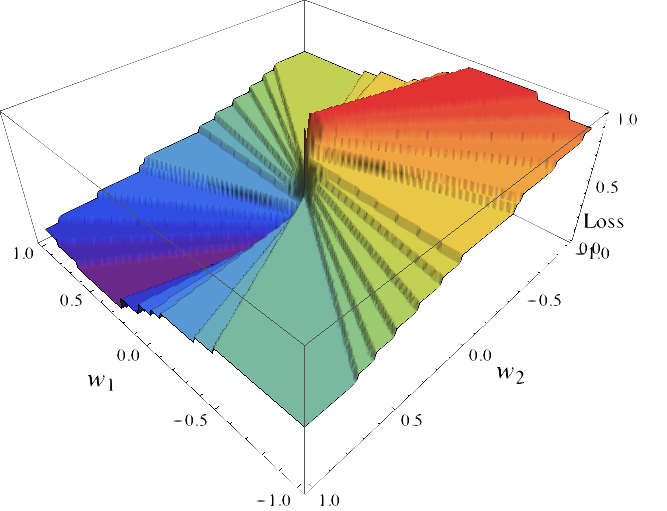
Not amenable to gradient-based methods.
Known to be NP-hard!
Feldman, Vitaly, et al. "Agnostic learning of monomials by halfspaces is hard." SIAM Journal on Computing (2012)
Greedy algorithms (Convex) relaxations
Nguyen, Tan, and Scott Sanner. "Algorithms for direct 0--1 loss optimization in binary classification." ICML 2013.
SVM, Logistic Regression, Boosting, etc.
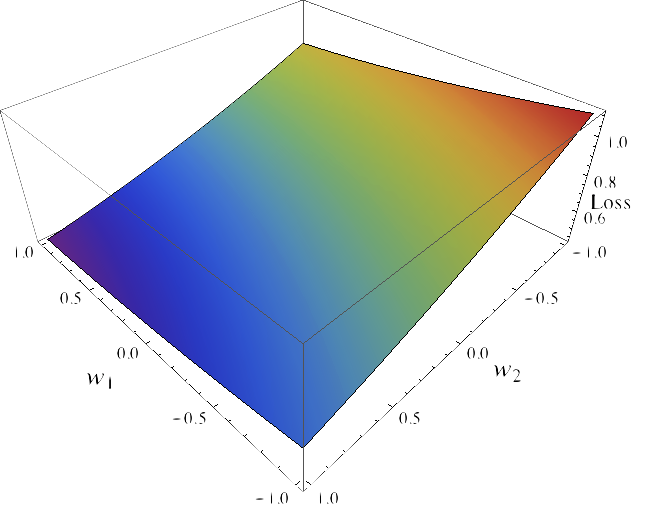
Convex relaxation
Replace the zero-one loss by a convex upper bound:
- a) $\frac{1}{n}\sum_{i}^n \ell(y_i w^T X_i)$

- b) $\frac{1}{n} \sum_{i}^n \psi(y_i X w))$, where $\psi(t) = \log(1 + e^{-t})$
Fisher consistency
Notation: $\mathcal{X}$ = sample space, $\mathcal{Y}$ = target values, $P$ = probability distribution on $\mathcal{X} \times \mathcal{Y}$
Population setting: suppose we have access to distribution $P$ that generates the sample $\{(X_1, y_1), \ldots, (X_n, y_n)\}$
- Original problem: $\argmin_h~ \mathbb{E}_{(X, Y) \sim P}(\ell(Y, h(X)))\quad$
- Surrogate: $\argmin_h~ \mathbb{E}_{(X, Y) \sim P}(\psi(Y, h(X)))\quad$
Fisher consistency:
- A surrogate $\psi$ is Fisher consistent if $f^*$ solution of surrogate $\implies$ $f^*$ solution to the original problem, i.e.
- $$h^* \in \argmin_{h}~ \mathbb{E}_{(X, Y) \sim P}(\psi(Y, h(X))) \implies$$ $$h^* \in \argmin_{h}~ \mathbb{E}_{(X, Y) \sim P}(\ell(Y, h(X)))$$
Fisher consistency
- Sometimes refered simply as consistency or classification calibration (related concept: asymptotic consistency, model consistency [e.g. Lasso]).
- Sheds light on the (surprisingly) good performance of SVM, Boosting, etc..
- Desirable but not necessary for good performance. Rifkin, Ryan, and Aldebaro Klautau. "In defense of one-vs-all classification." The Journal of Machine Learning Research 5 (2004): 101-141.
- First results from Lin, Y. (2001). A note on margin-based loss functions in classification. Technical Report 1044r, later extended by Tong Zhang, Peter Bartlett and others.
Results binary-class
Theorem: Let $\psi$ be convex. Then $\psi$ is classification-calibrated if and only if it is differentiable at 0 and $\psi'(0) \lt 0$
Bartlett, P. L., Jordan, M. I., & McAuliffe, J. D. (2003). Convexity , Classification , and Risk Bounds. Journal of the American Statistical Association.

- Depends on the derivative at a single point.
- Some methods (e.g. SVM) are consistent despite not estimating probabilities
Multiclass
"... most of popular loss functions for binary classification are Fisher-consistent"
Zou, H., Zhu, J., & Hastie, T. (2008). New multicategory boosting algorithms based on multicategory Fisher-consistent losses. The Annals of Applied Statistics
Different approaches for SVM multiclass
One-vs-one $\implies$ consistent
One-vs-rest $\implies$ inconsistent
Liu, Y. (2007). Fisher Consistency of Multicategory Support Vector Machines. In NIPS 2007 (pp. 1–8).
Concept of non-dominant distribution
$P$ is called non-dominant if $P(y|X) \lt \frac{1}{2}$ for all $y \in \mathcal{X}$
Outline
- 1. Binary class classification.
- Bartlett, P. L., Jordan, M. I., & McAuliffe, J. D. (2003). Convexity , Classification , and Risk Bounds. Journal of the American Statistical Association.
- 2. Ordinal regression.
- Pedregosa, F., Bach, F., Gramfort, A., “On the Consistency of Ordinal Regression Methods.”, ArXiv 2015
- 3. Ranking.
- Duchi, J. C., Mackey, L. W., & Jordan, M. I. (2010). On the Consistency of Ranking Algorithms. ICML 2010
- 4. Open problem
Ordinal regression
Setting: same as multiclass classification, but labels have an order information.
- My motivation: predict the size of objects from fMRI images Borghesani, V. et al. (2014). A perceptual-to-conceptual gradient of word coding along the ventral path. PRNI.

- Often applicable when target value consists of human-generated rating: movie-ratings, pain levels, etc.
- Basic model proposed in the 80s: proportional odds [P. McCullagh 1980]
Ordinal regression
How to include the order information within the model?
Probabilistic point of view:
$P(y \leq i | X) = \text{sigmoid}(f(X)) \quad $[McCullagh 1980]
Optimization point of view:
Minimize a convex surrogate of $\ell^{\text{OR}}(y, \hat{y}) = |y - \hat{y}|$ (absolute error)
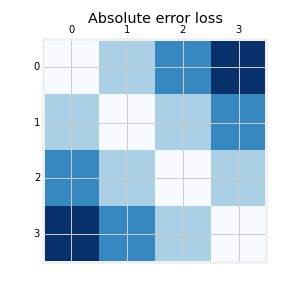
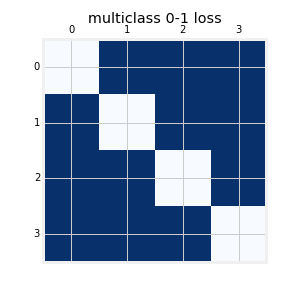
Ordinal regression
Learn: $f: \mathcal{X} \to \RR^{k-1}$ ($k$ = num. of classes)
Prediction: $1 + \sum_{i=1}^{k-1} \ell(f(X)_i) $
$\implies \ell^{\text{OR}}(y, f(X))$ = $|y - 1 + \sum_{i=1}^{k-1} \ell(f(X)_i)|$
$= \sum_{i=1}^{y-1} \ell(-f(X)_i) + \sum_{i=y}^{k-1} \ell(f(X)_i)$
A natural surrogate is given by
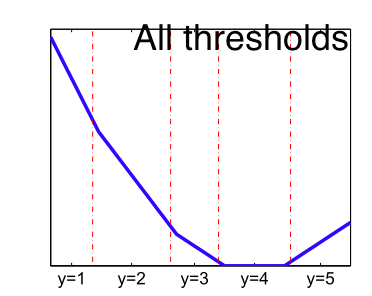
All Thresholds (AT) $\sum_{i=1}^{y-1} \psi(-f(X)_i) + \sum_{i=y}^{k-1} \psi(f(X)_i)$
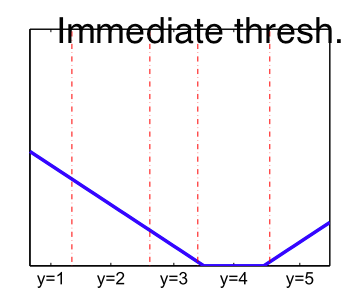
But Immediate Thresholds (IT) has also been proposed $\psi(-f(X)_{y-1}) + \psi(f(X)_y)$
Empirical comparison
- [Rennie & Srebro 2005]
- [Chu & Keerthi 2005]
- [Lin & Li 2006]
Is there a reason that can explain this behaviour ?
Mean Absolute Error
So according to these studies it seems that that loss functions of the form b) perform better on the datasets they tried. Question: should we assume that because it performed better on some datasets b) is superior to a) ?.
The results that we will give in this section provide theoretical insight on this question.
Threshold-based surrogates
Propose a formulation that parametrizes both surrogates
$$\Psi^{\ell}(y, f(X)) = \sum_{i = 1}^{y-1} \Delta \ell(y, i)\psi(f(X)_i) - \sum_{i=y}^{k-1}\Delta \ell(y, i)\psi(-f(X)_i)$$
where
- $\Delta\ell(y, i) = \ell(y,i+1) - \ell(y, i)$
- $\psi: \RR \to \RR$ is a binary-class surrogate loss function (hinge, logistic, etc.).
- For $\ell$ = zero-one loss $\implies$ $\psi^{\ell}$ = Immediate Threshold (IT).
- For $\ell$ = absolute error loss $\implies$ $\psi^{\ell}$ = All Threshold (AT).
Consistency of $\psi^{\ell}$
$\Psi^{\ell}(y, f(X)) = \sum_{i = 1}^{y-1} \Delta \ell(y, i)\phi(f(X)_i) - \sum_{i=y}^{k-1}\Delta \ell(y, i)\phi(-f(X)_i)$
- Main result
- if $\phi$ is differentiable at zero and $\phi'(0) < 0$
- $\implies$ the surrogate $\Psi^{\ell}$ is consistent with respect to $\ell$
- All Threshold) $\sum_{i=1}^{y-1}{\phi}(-f(X)_{i}) + \sum_{i=y}^k {\phi}(f(X)_i)$ $\implies$ consistent w.r.t. absolute error
- Immediate Threshold) ${\phi}(-f(X)_{y-1}) + {\phi}( f(X)_y)$ $\implies$ consistent w.r.t. 0-1 loss
Illustration
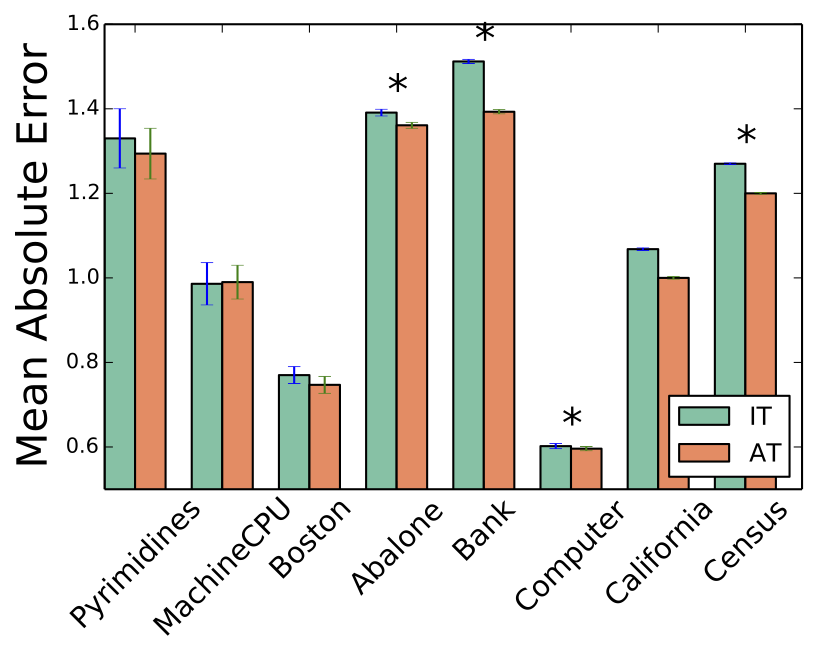
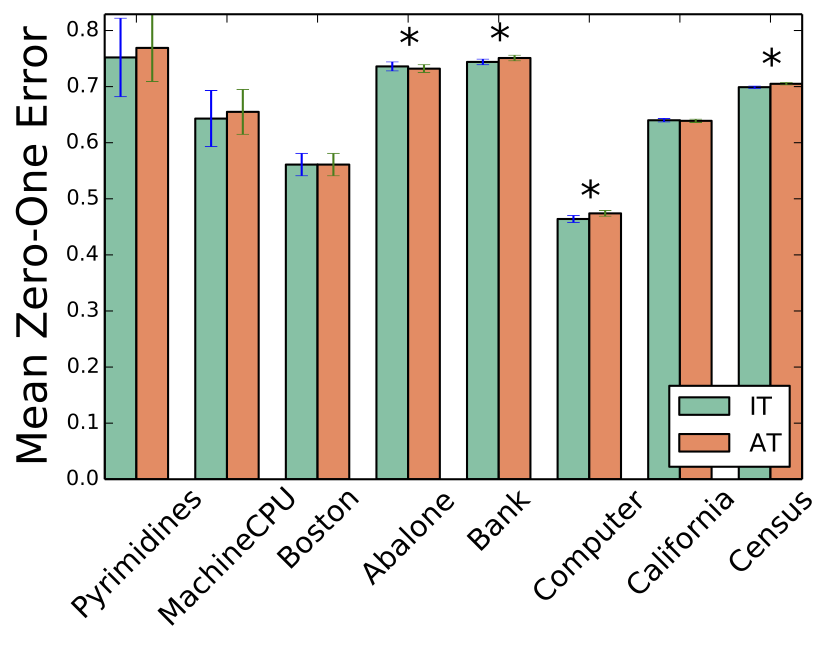
- Hinge loss
- 8 Datasets
- AT performs better w.r.t Absolute Error
- IT performs better w.r.t. Zero-One Error
Outline
- 1. Binary class classification.
- Bartlett, P. L., Jordan, M. I., & McAuliffe, J. D. (2003). Convexity , Classification , and Risk Bounds. Journal of the American Statistical Association.
- 2. Ordinal regression.
- Pedregosa, F., Bach, F., Gramfort, A., “On the Consistency of Ordinal Regression Methods.”, ArXiv 2015
- 3. Ranking.
- Duchi, J. C., Mackey, L. W., & Jordan, M. I. (2010). On the Consistency of Ranking Algorithms. ICML 2010
- 4. Open problem
Ranking
Motivation: search results ranking.
Information of clickthrough data:
$X_i$ = $i$-th search result
$X_3 > X_2$ and $X_4 > X_2$
"... clickthrough data does not convey absolute relevance judgments, but partial relative relevance judgments ...", Joachims, T. (2002). Optimizing Search Engines using Clickthrough Data. ACM SIGKDD.
(pairwise) Ranking
Goal
Given: partial relevance judgements
Learn a function $f: \mathcal{X} \to \RR$ such that:$f(X_i) \gt f(X_j)$ if $X_i > X_j$.
$\implies$ sort the webpages such that $f(X_a) \geq f(X_b) \geq f(X_c) \ldots$
Ranking
Pairwise disagreement loss: Given a Directed Acyclical Graph $G$, $$\ell(G, f(X)) = \sum_{i \to j \in G} \ell(f(X_i) - f(X_j)) $$
Surrogate:$$\psi(G, f(X)) = \sum_{i \to j \in G} \phi(f(X_i) - f(X_j)) $$
Where $\phi$ is a surrogate of the 0-1 loss. For $\phi$=hinge loss, it is known as RankSVM.
Objective: $$ \argmin_f \mathbb{E}_{X, G}[\ell(G, f)]$$
Ranking
Surrogate:$$\psi(G, f(X)) = \sum_{i \to j \in G} \phi(f(X_i) - f(X_j)) $$
Result: commonly used surrogates (e.g. RankSVM) are inconsistent
Theorem: if surrogate loss is consistent, then it is non-convex.
Duchi, J. C., Mackey, L. W., & Jordan, M. I. (2010). On the Consistency of Ranking Algorithms. In Proceedings of the 27th International Conference on Machine Learning.
Direct proof and extended to other ranking loss functions Calauzènes, C., Usunier, N., & Gallinari, P. (2012). On the ( Non- ) existence of Convex , Calibrated Surrogate Losses for Ranking. NIPS 2012.
Outline
- 1. Binary class classification.
- Bartlett, P. L., Jordan, M. I., & McAuliffe, J. D. (2003). Convexity , Classification , and Risk Bounds. Journal of the American Statistical Association.
- 3. Ordinal regression.
- Pedregosa, F., Bach, F., Gramfort, A., “On the Consistency of Ordinal Regression Methods.”, ArXiv 2015
- 4. Ranking.
- Duchi, J. C., Mackey, L. W., & Jordan, M. I. (2010). On the Consistency of Ranking Algorithms. ICML 2010
- 5. Open problem
Open problem: $\mathcal{F}$-consistency
- $\mathcal{F}$-consistency (a.k.a. parametric consistency):
- $$h^* \in \argmin_{h {\color{red} \in \mathcal{F}}} ~ \mathbb{E}_{(X, Y) \sim P}(\psi(Y, h(X))) \implies$$ $$h^* \in \argmin_{h {\color{red} \in \mathcal{F}} }~ \mathbb{E}_{(X, Y) \sim P}(\ell(Y, h(X)))$$
$\mathcal{F}$ can be e.g. the space of smooth functions.
Result: Given $\mathcal{F}$ "regular" (Im($\mathcal{F}$) = $\RR$): $\mathcal{F}$-consistency $\implies$ consistency
Shi, Q., Reid, M., Caetano, T., & Hengel, A. Van Den. (2014). A Hybrid Loss for Multiclass and Structured Prediction (TPAMI)
Thanks for your attention
Co-authors
Francis Bach 
Alexandre Gramfort 
Backup
Relationship with other properties
- Fisher consistency in classical statistics:
- Estimator of $\theta$ is a functional of the empirical distribution function $\hat{F}_n$: $\hat{\theta} = T(\hat{F}_n)$
- Same concept of Fisher consistency [Fisher 1925] of an estimator in classical statistics, where the parameter is the Bayes risk: $\inf_{h}~ \mathbb{E}_{(X, Y) \sim P}(\ell(Y, h(X)))$.
- Other consistency in machine learning:
Absolute Error
Models: Least Absolute Error, Ordinal Logistic Regression , Multiclass Classification
Least Absolute Error
Model parameters: $\mathbf{w} \in \RR^p, b \in \RR$
Decision function: $f(\mathbf{x}_i) = b + \langle \mathbf{x}_i, \mathbf{w} \rangle$
Prediction: $\text{round}_{1 \leq i \leq k} (f(\mathbf{x}_i))$
Estimation: $\mathbf{w}^*, b^* \in \argmin_{\mathbf{w}, b} \frac{1}{n}\sum_{i=1}^n |y_i - f(\mathbf{x}_i)| + \lambda \|\mathbf{w}\|^2$
Regression model in which the prediction is given by rounding to the closest label.