Your browser doesn't support the features required by impress.js, so you are presented with a simplified version of this presentation.
For the best experience please use the latest Chrome, Safari or Firefox browser.
Frank-Wolfe algorithm for constrained convex optimization
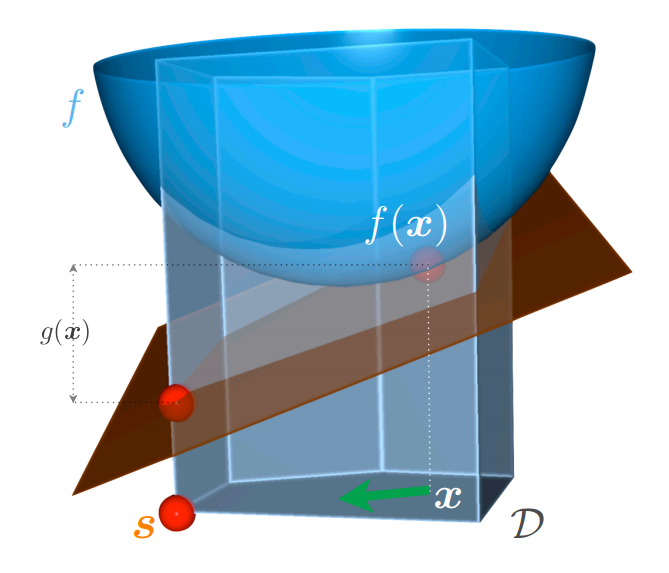
Image: Jaggi et al. 2013
Fabian Pedregosa, Parietal Meeting September 2013
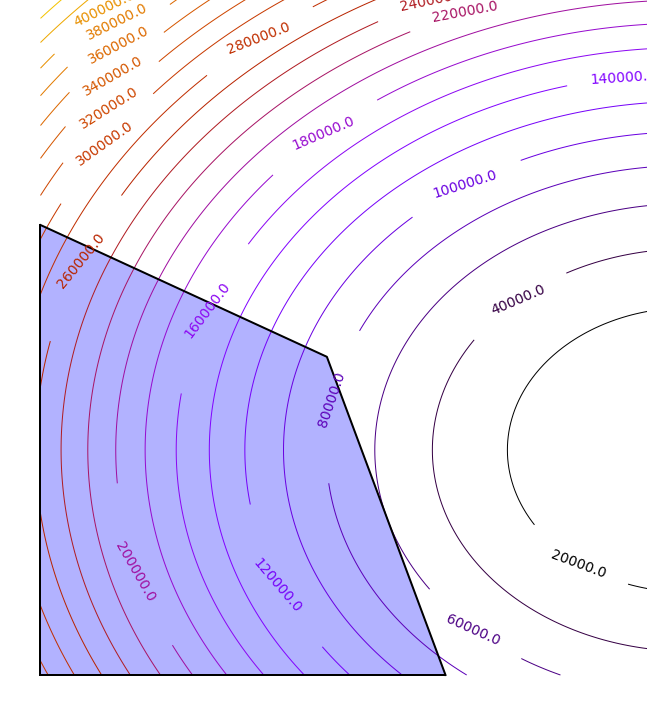
Context: Optimization problems of the form
$$ \underset{x \in \mathcal{D}}{\operatorname{argmin}} f(x) $$
where $f$ is convex differentiable
and the domain $\mathcal{D}$ is convex compact.
Applicable to problems such as
- Lasso
- Group Lasso
- Trace norm
- Total Variation
Belongs to the family of gradient-based (first order) methods as
- Projected Gradient Descent
- Proximal Methods
Algorithm
- Let $x^{(0)} \in \mathcal{D}$
- for $k = 0 ... K$ do
- Compute $s = \underset{s' \in \mathcal{D}}{\operatorname{argmax}}
\langle s', - \nabla f(x^{(k)}) \rangle$
- Let $\gamma = \frac{2}{k+2}$ or optimize $\gamma$ by line-search
- Update $x^{(k+1)} = (1 - \gamma) x^{(k)} + \gamma s$
Complexity
[Wolfe 1956, Jaggi 2013] say $$f(x^{(k)}) - f(x^*) \leq \frac{2 C_f}{k + 2} = \mathcal{O}\left( \frac{1}{k} \right)$$
i.e. similar to (unaccelerated) proximal gradient algorithms
But running time it depends on how fast you can solve the subproblem
$$s = \underset{s' \in \mathcal{D}}{\operatorname{argmax}}
\langle s', - \nabla f(x^{(k)}) \rangle$$
which might be a hard problem ...
But for domains $\mathcal{D}$ that are convex envelope of another set $\mathcal{A}$,
then
$$
\underset{s' \in \mathcal{D}}{\operatorname{sup}}
\langle s', y \rangle = \underset{s' \in \mathcal{A}}{\operatorname{sup}}
\langle s', y \rangle
$$
For example:
- Instead of optimizing over the unit $\ell_1$-ball ...
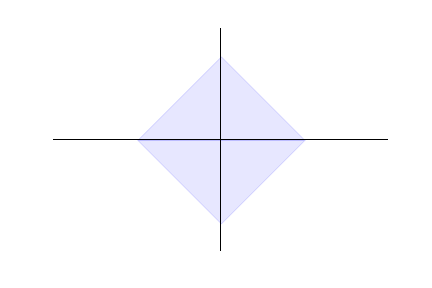
You optimize over the canonical vectors
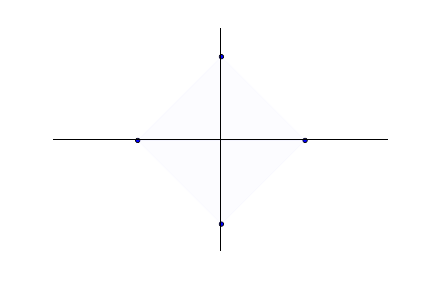
- Instead of optimizing over the unit nuclear-norm ball (trace-norm ball) ...
You optimize over the set of rank-one matrices
(leading singular vector, solvable by Power or Lanczos iteration)
Approximately solving the subproblem
Approximately solve the subproblem
$$
s = \underset{s' \in \mathcal{D}}{\operatorname{argmin}}
\langle s', \nabla f(x^{(k)}) \rangle
$$
Such that
$
\langle s, \nabla f(x^{(k)}) \rangle \leq
\underset{s' \in \mathcal{D}}{\operatorname{min}}
\langle s, \nabla f(x^{(k)}) \rangle + \frac{1}{2} \delta C_f
$
And you still get linear convergence
$$f(x^{(k)}) - f(x^*) \leq \frac{2 C_f}{k + 2}\color{red}{(1 + \delta)}$$
On real data
Dataset: Kay 2008 (Natural Images)
Model: trace-norm penalized linear regression. $ \|y - X \text{vec}(B) \|^2 \text{ subject to } \|B\|_* \leq 1$
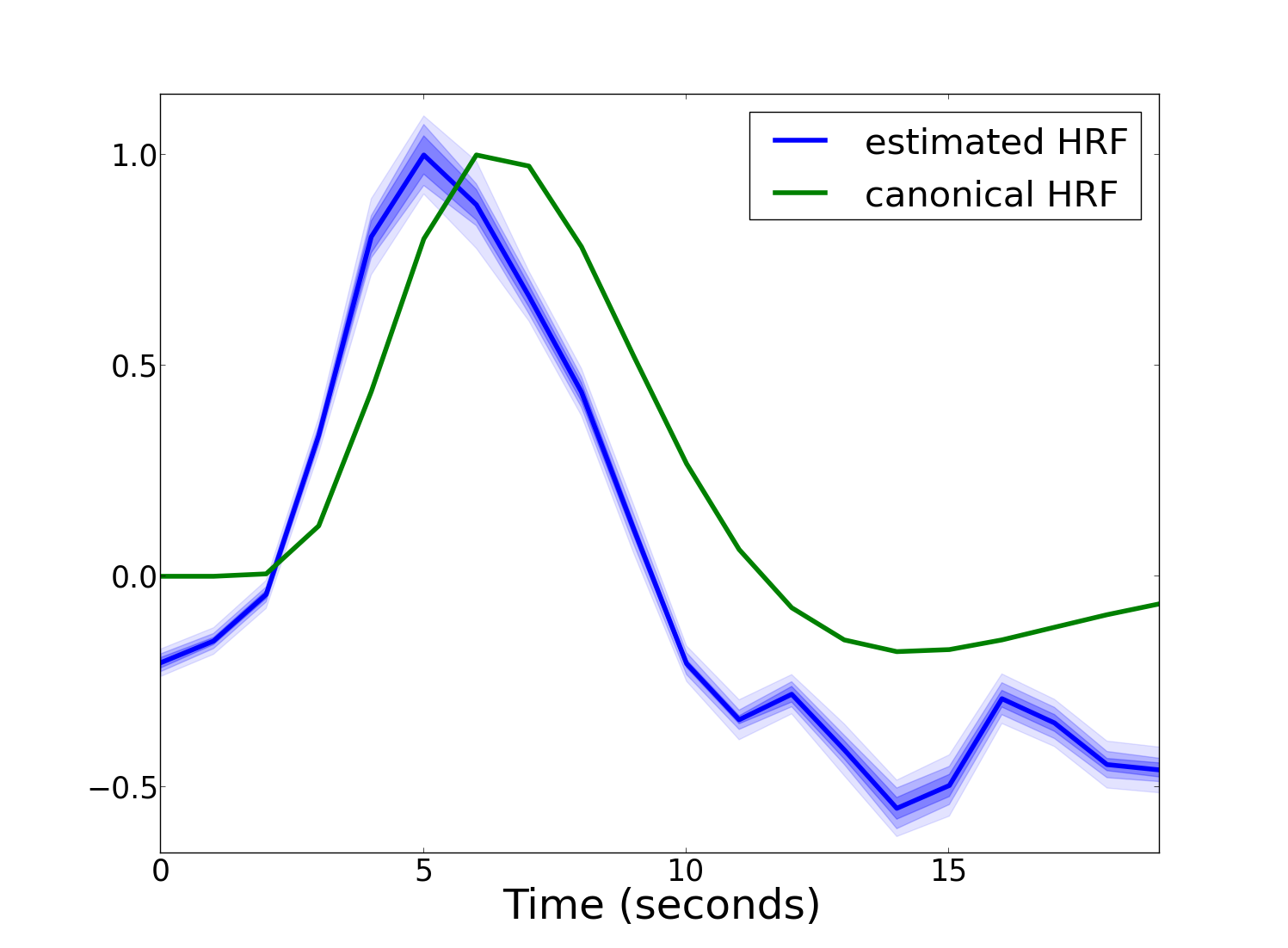
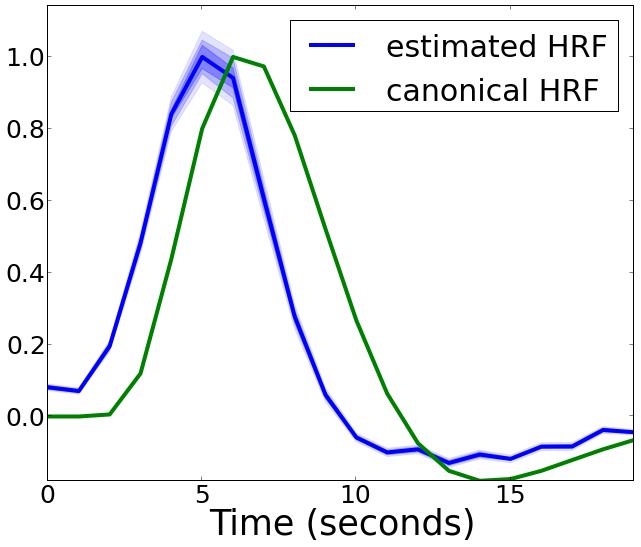
Convex Formulation
Non-Convex Formulation
References
- An algorithm for quadratic programming,
M Frank, P Wolfe - Naval research logistics quarterly, 1956
- Revisiting Frank-Wolfe: Projection-Free Sparse Convex Optimization,
Martin Jaggi
- Block-Coordinate Frank-Wolfe Optimization for Structural SVMs
,
Simon Lacoste-Julien, Martin Jaggi, Mark Schmidt, Patrick Pletscher 2013