Feature extraction and supervised learning on fMRI:

from practice to theory

Fabian Pedregosa-Izquierdo, Parietal/Sierra (INRIA)

Advisors	Francis Bach	INRIA/ENS, Paris, France.
	Alexandre Gramfort	Telecom Paristech, Paris, France.
Reviewers	Dimitri Van de Ville	Univ. Geneva / EPFL, Geneva, CH.
	Alain Rakotomamonjy	University of Rouen, Rouen, France.
Examiners	Ludovic Denoyer	UPMC, Paris, France.
	Marcel A.J. van Gerven	Donders Institute/Radboud Univ., NL.
	Bertrand Thirion	INRIA/CEA, Saclay, France.

Study of cognitive function

Before the advent of non-invasive imaging modalities.

Patients

Lesions

Post-mortem analysis

Finding

Post-mortem analysis of “Tan” [Paul Broca, 1861]

1 / 35

fMRI-based study

Blood-oxygen-level dependent (BOLD) signal

Processing pipeline

Friederici, A. D. (2011) “The brain basis of language processing: from structure to function”. Physiological reviews

2 / 35

fMRI-based study

Blood-oxygen-level dependent (BOLD) signal

Processing pipeline
Preprocessing
Feature Extraction
Univariate Statistics
Supervised Learning

Answer increasingly complex cognitive questions.

E. Cauvet, “Traitement des structures syntaxiques dans le langage et dans la musique”, PhD thesis.

3 / 35

Feature extraction

Input: BOLD signal and an experimental paradigm.

Goal: output time-independent activation coefficients.

Delayed nature of the hemodynamic response (HRF).

4 / 35

Supervised Learning - Decoding

Predict stimuli from activation coefficients.

Contribution: decoding with ordinal values.

5 / 35

Outline

1. Data-driven HRF estimation with R1-GLM.
- Pedregosa, Eickenberg et al. “Data-driven HRF estimation for encoding and decoding models.”, Neuroimage, Jan. 2015.
- Pedregosa, Eickenberg et al. “HRF estimation improves sensitivity of fMRI encoding and decoding models” PRNI 2013
2.
Decoding with ordinal labels
- Pedregosa et al., “Learning to rank from medical imaging data,” MLMI 2012.
- Pedregosa et al., “Improved Brain Pattern Recovery through Ranking Approaches”, 2012.

3. Fisher consistency of ordinal regression models.
- Pedregosa et al., “On the Consistency of Ordinal Regression Methods.”, ArXiv 2014

6 / 35

The General Linear Model (GLM)

where $X_i = \quad \quad~ \ast~ \text{s}_i(t)$

7 / 35

Basis-constrained HRF

Hemodynamic response function (HRF) is known to vary substantially across subjects, brain regions and age.

D. Handwerker et al., “Variation of BOLD hemodynamic responses across subjects and brain regions and their effects on statistical analyses.,” Neuroimage 2004.

S. Badillo et al., “Group-level impacts of within- and between-subject hemodynamic variability in fMRI,” Neuroimage 2013.

Two basis-constrained models of the HRF: FIR and 3HRF.

8 / 35

R1-GLM

$\beta_1$

$h_1$

$\beta_1$

$h_2$

$\beta_1$

$h_3$

$\beta_2$

$h_4$

$\beta_2$

$h_5$

$\beta_2$

$h_6$

$\cdots$

$\beta_{k}$

$h_{3k-2}$

$\beta_{k}$

$h_{3k-1}$

$\beta_k$

$h_{3k}$

9 / 35

Validation of R1-GLM

Improvement using decoding and encoding models.

10 / 35

Results

Cross-validation score in two different datasets

S. Tom et al., “The neural basis of loss aversion in decision-making under risk,” Science 2007.

K. N. Kay et al., “Identifying natural images from human brain activity.,” Nature 2008.

Results - Encoding

Measure: voxel-wise encoding score. Correlation with the BOLD at each voxel on left-out data.
R1-GLM (FIR basis) improves voxel-wise encoding score on more than 98% of the voxels.

11 / 35

Conclusions

Model for the joint estimation of HRF and activation coefficients.
Constrained estimation of the HRF while remaining computationally tractable (~1h for full brain estimation).
Validated the pertinence of this model by improvement in decoding and encoding score obtained on two fMRI datasets.
Article and software distribution
“Data-driven HRF estimation for encoding and decoding models.,” Pedregosa, Eickenberg et al., Neuroimage, Jan. 2015.
hrf_estimation: http://pypi.python.org/pypi/hrf_estimation

12 / 35

Outline

1. Data-driven HRF estimation with R1-GLM.
- Pedregosa, Eickenberg et al. “Data-driven HRF estimation for encoding and decoding models.”, Neuroimage, Jan. 2015.
- Pedregosa, Eickenberg et al. “HRF estimation improves sensitivity of fMRI encoding and decoding models” PRNI 2013
2.
Decoding with ordinal labels
- Pedregosa et al., “Learning to rank from medical imaging data,” MLMI 2012.
- Pedregosa et al., “Improved Brain Pattern Recovery through Ranking Approaches”, 2012.

3. Fisher consistency of ordinal regression models.
- Pedregosa et al., “On the Consistency of Ordinal Regression Methods.”, ArXiv 2014

13 / 35

Decoding with ordinal labels

$\mathbf{X} \quad \to \quad \mathbf{y}$

Activation coefficients

Target values

Target values can be

Binary $\{-1, 1\}$
Continuous $\{0.34, 1,3, \ldots \}$
Ordinal: $\{1, 2, 3, \ldots, k\}$ , $1 \prec 2 \prec 3$ ...

How can we incorporate the order information into a decoding model ?

14 / 35

Loss functions

Two relevant loss functions:

$\ell_{\mathcal{A}}(y, \hat{y}) = | y - \hat{y}|$ .
Measures the distance betwen the predicted and true label.
Models: Ordinal Logistic Regression, Least Absolute Error, Cost-sensitive Multiclass

$\ell_{\mathcal{P}}(y_1, y_2, \hat{y}_1, \hat{y}_1) =$ 0 if $\text{sign}(y_1-y_2)$ = $\text{sign}(\hat{y}_1 - \hat{y}_2))$ , 1 otherwise.
Measures ordering betweem $(y_1, y_2)$ and $(\hat{y}_1, \hat{y}_2)$ .
Models: LogisticRank

2 loss functions $\implies$ 2 aspects of the ordinal problem.

15 / 35

Ordinal Logistic Regression

J. Rennie and N. Srebro, “Loss Functions for Preference Levels : Regression with Discrete Ordered Labels,” IJCAI 2005.

Generalization of logistic regression.

Parameters ( $p$ = num. dimensions, $k$ = num. classes)

coefficients $\mathbf{w} \in \RR^p$
$\boldsymbol{\theta} \in \RR^{k-1}$

Prediction

1 + $\argmin\{i: \mathbf{w}^T \mathbf{x} > \theta_i \}$

Surrogate loss function:

$\sum_{j=1}^{y-1} \text{logistic}(\theta_j-\mathbf{w}^T \mathbf{x}) + \sum_{j=y}^{k-1} \text{logistic}(\mathbf{w}^T \mathbf{x} - \theta_j)$

16 / 35

Pairwise ranking

R. Herbrich et al., “Support Vector Learning for Ordinal Regression,” 1999.
T. Joachims, “Optimizing Search Engines using Clickthrough Data,” SIGKDD 2002.

Parameters ( $p$ = num. dimensions, $k$ = num. classes)

coefficients $\mathbf{w} \in \RR^p$

: $\text{sign} (\mathbf{w}^T \mathbf{x}_i - \mathbf{w}^T\mathbf{x}_j) = \text{sign} (\mathbf{w}^T(\mathbf{x}_i - \mathbf{x}_j))$

Surrogate loss function

$\text{logistic} (\text{sign}(y_i - y_j)(\mathbf{w}^T (\mathbf{x}_i - \mathbf{x}_j)))$

$\implies$ can be implemented as a binary-class logistic regression model, $\hat{y}_{ij} = y_i - y_j, \hat{\mathbf{x}}_{ij} = \mathbf{x}_i - \mathbf{x}_j$

17 / 35

Two fMRI datasets, three tasks

1) Predict level of complexity of a phrase (6 levels)

E. Cauvet, Traitement des structures syntaxiques dans le langage et dans la musique, PhD thesis

2) Predict number of letters in a word.

3) Predict real size of objects from noun.

V. Borghesani, “A perceptual-to-conceptual gradient of word coding along the ventral path,” PRNI 2014.

18 / 35

Results - Mean Absolute Error

Top performers:

Ordinal Logistic
Least Absolute Error.

19 / 35

Results - Pairwise Disagreement

Top performer: RankLogistic

Application: role of language ROIs in complexity of sentences.

F. Pedregosa et al., “Learning to rank from medical imaging data,” MLMI 2012.

20 / 35

Conclusions

Two loss functions for the task of decoding with ordinal values.
Using 4 different models, use order information in context of fMRI-based brain decoding.
Benchmarked the methods on 3 tasks (2 datasets).
First usage of pairwise ranking in the context of fMRI, software distribution.
“Learning to rank from medical imaging data,” Pedregosa et al. MLMI 2012.
PySofia: https://pypi.python.org/pypi/pysofia

21 / 35

Outline

1. Data-driven HRF estimation with R1-GLM.
- Pedregosa, Eickenberg et al. “Data-driven HRF estimation for encoding and decoding models.”, Neuroimage, Jan. 2015.
- Pedregosa, Eickenberg et al. “HRF estimation improves sensitivity of fMRI encoding and decoding models” PRNI 2013
2.
Decoding with ordinal labels
- Pedregosa et al., “Learning to rank from medical imaging data,” MLMI 2012.
- Pedregosa et al., “Improved Brain Pattern Recovery through Ranking Approaches”, 2012.

3. Fisher consistency of ordinal regression models.
- Pedregosa et al., “On the Consistency of Ordinal Regression Methods.”, ArXiv 2014

22 / 35

Ordinal Regression surrogates

${\text{logistic}}(f(X) - \theta_{y-1}) + {\text{logistic}}(\theta_{y} - f(X))$
$\sum_{i=1}^{y-1}{\text{logistic}}(f(X) - \theta_{i}) + \sum_{i=y}^k {\text{logistic}}(\theta_{i} - f(X))$
J. Rennie and N. Srebro, “Loss Functions for Preference Levels : Regression with Discrete Ordered Labels,” IJCAI 2005.

23 / 35

${\color{BlueViolet}\text{hinge}}(f(X) - \theta_{y-1}) + {\color{BlueViolet}\text{hinge}}(\theta_{y} - f(X))$
$\sum_{i=1}^{y-1} {\color{BlueViolet}\text{hinge}}(f(X) - \theta_{i}) + \sum_{i=y}^k {\color{BlueViolet}\text{hinge}}(\theta_{i} - f(X))$
W. Chu and S. S. Keerthi, “New approaches to Support Vector Ordinal Regression,” ICML 2005.

${\color{BlueViolet}\text{exp}}(-(f(X) - \theta_{y-1})) + {\color{BlueViolet}\text{exp}}(-(\theta_{y} - f(X)))$
$\sum_{i=1}^{y-1}{\color{BlueViolet}\text{exp}}(-(f(X) - \theta_{i})) + \sum_{i=y}^k {\color{BlueViolet}\text{exp}}(-(\theta_{i} - f(X)))$
H. Lin and L. Li, “Large-Margin Thresholded Ensembles for Ordinal Regression : Theory and Practice,” Algorithmic Learning Theory 2006.

Empirical comparison

[Rennie & Srebro 2005]
[Chu & Keerthi 2005]
[Lin & Li 2006]

Is there a reason that can explain this behaviour ?

Mean Absolute Error

24 / 35

Fisher consistency

minimize : $\begin{equation} \label{eq:l_risk} \mathcal{R}_{\ell}(h) = \mathbb{E}(\ell(Y, h(X)))\quad. \end{equation}$
$\implies$ computationally intractable. Minimize the $\mathcal{R}_{\psi}(h) = \mathbb{E}(\psi(Y, h(X)))$

Fisher consistency:

Relate minimizer of $\mathcal{R}_{\psi}$ with the minimizer of $\mathcal{R}_{\ell}$ .
$f^* \in \argmin_{f \in \mathcal{F}} \mathcal{R}_{\psi}(f) \implies \mathcal{R}_{\ell}(f^*) = \mathcal{R}_{\ell}(h^*)$ where $h^*$ is a minimizer of the risk (Bayes rule)

25 / 35

Illustration

Binary-class linear problem on $\RR^2$

a) $\sum_{i}^n \ell(y_i, h(X_i))$

b) $\sum_{i}^n \text{logistic}(y_i X w))$

26 / 35

Fisher consistency

Previous work

Binary classification
P. Bartlett et al., “Convexity , Classification , and Risk Bounds,” J. Am. Stat. Assoc. 2003.
Pairwise ranking
J. Duchi et al., “On the Consistency of Ranking Algorithms,” ICML 2010.
Ordinal Regression
Pedregosa et al., “On the Consistency of Ordinal Regression Methods.”, ArXiv preprint, Nov. 2014

27 / 35

Threshold-based surrogates

Propose a formulation that parametrizes the ordinal regression surrogates seen so far

$\psi^{\ell}(y, \boldsymbol{\alpha}) = \sum_{i = 1}^{y-1} \Delta \ell(y, i)\phi(\alpha_i) - \sum_{i=y}^{k-1}\Delta \ell(y, i)\phi(-\alpha_i)$

where

$\Delta\ell(y, i) = \ell(y,i+1) - \ell(y, i)$
$\phi: \RR \to \RR$ is a binary-class surrogate loss function (hinge, logistic, etc.).

For $\ell$ = zero-one loss $\implies$ $\psi^{\ell}$ = Immediate Threshold (IT).
For $\ell$ = absolute error loss $\implies$ $\psi^{\ell}$ = All Threshold (AT).

28 / 35

Consistency of $\psi^{\ell}$

$\psi^{\ell}(y, \boldsymbol{\alpha}) = \sum_{i = 1}^{y-1} \Delta \ell(y, i)\phi(\alpha_i) - \sum_{i=y}^{k-1}\Delta \ell(y, i)\phi(-\alpha_i)$

Main result
${\phi: \RR \rightarrow \RR_+}$ consistent with respect to the zero-one binary loss, i.e., $\phi$ is differentiable at zero and $\phi'(0) < 0$
$\implies$ the surrogate $\psi^{\ell}$ is consistent with respect to $\ell$

${\phi}(f(X) - \theta_{y-1}) + {\phi}(\theta_{y} - f(X))$ $\implies$ consistent w.r.t. 0-1 loss
$\sum_{i=1}^{y-1}{\phi}(f(X) - \theta_{i}) + \sum_{i=y}^k {\phi}(\theta_{i} - f(X))$ $\implies$ consistent w.r.t. absolute error

29 / 35

Illustration

Hinge loss
8 Datasets

AT performs better w.r.t Absolute Error
IT performs better w.r.t. Zero-One Error

30 / 35

Other results

Consistency

Absolute Error surrogate: ( $\psi_{\mathcal{A}}(y, \alpha) = |y - \alpha|$ )
Consistent w.r.t. Absolute Error
Extends results of [H. Ramaswamy 2012]
Squared Error surrogate: $\psi_{\mathcal{S}}(y, \alpha) = (y - \alpha)^2$
Consistent w.r.t. Squared Error
Proportional odds : $P(y \leq i | X) = \sigma(\theta_i - X w)$
Consistent w.r.t. Absolute Error

31 / 35

Contributions

1. Data-driven HRF estimation with R1-GLM.
- Model for the joint estimation of HRF and activation coefficients.
- Constrained estimation of the HRF, validated on several fMRI datasets
2. Decoding with ordinal labels.
- Examine two different metrics for the problem of decoding with ordinal labels.
- Compare different models that optimize a surrogate of this criterion.
3. Fisher consistency of ordinal regression models.
- Studied consistency of a large family of surrogate loss functions for the context of ordinal regression.

32 / 35

Perspectives

computational cost of R1-GLM

$\argmin_{\mathbf{h}, ~\boldsymbol{\beta}} \|\mathbf{y} - \mathbf{X} \text{vec}(\mathbf{h}\boldsymbol{\beta}^T)\|^2$

Common user case: > 50.000 voxels.

Unused structure:

Repeated design ( $\mathbf{X}$ ).
Spatial smoothness.

More realistic noise model.

33 / 35

Perspectives

Consistency in a constrained space.

Current proof implicitly assumes decision functions can be separately defined for each sample.
Threshold-based decision functions are of the form $(\theta_1 - f(X), \theta_2 - f(X), \ldots, \theta_{k-1} - f(X))$ .
$\boldsymbol{\theta}$ is shared among all samples.
Is it possible to obtain consistency results in this setting ?

34 / 35

Thanks for your attention

35 / 35

Backup slides

The Linear-Time-Invariant assumption

The model of the BOLD signal that is commonly used assumes a linear-time-invariant relationship between the BOLD signal and the neural response.

Source: [Poldrack et al. 2011]

Homogeneity: If a neural response is scaled by a factor of $a$ , then the BOLD response is also scaled by this same factor of $a$ .
Additivity: The response for two separate events is the sum of the independent signals.
Time invariant: If a stimulus is shifted $t$ seconds, the BOLD response will be shifted by this same amount.

HRF variability

Across age
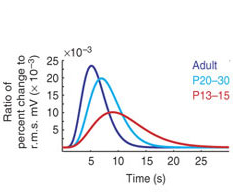
Across age: Matthew T. Colonnese, et al. “Development of hemodynamic responses and functional connectivity in rat somatosensory cortex”. Nature neuroscience 2007

Extension to separate designs

GLMS: Extension of the classical GLM proposed by [Mumford et al. 2012] that improves estimation in highly correlated designs.

R1-GLM with separate designs: R1-GLMS

Optimization problem of the form

$\sum_i^k \|\mathbf{y} - \beta_i \mathbf{X}^0_{\text{BS}i} \mathbf{h} - r_i \mathbf{X}^1_{\text{BS}i} \mathbf{h}\| ^2$

Subject to $\|\mathbf{B} \mathbf{h}\|_{\infty} = 1$ and $\langle \mathbf{h}, \mathbf{h}_{\text{ref}} \rangle > 0$

Source: [Mumford et al. 2012]

Results - Encoding

Results - Decoding

Absolute Error

Models: Least Absolute Error, Ordinal Logistic Regression , Multiclass Classification

Least Absolute Error

: $\mathbf{w} \in \RR^p, b \in \RR$

: $f(\mathbf{x}_i) = b + \langle \mathbf{x}_i, \mathbf{w} \rangle$

: $\text{round}_{1 \leq i \leq k} (f(\mathbf{x}_i))$

: $\mathbf{w}^*, b^* \in \argmin_{\mathbf{w}, b} \frac{1}{n}\sum_{i=1}^n |y_i - f(\mathbf{x}_i)| + \lambda \|\mathbf{w}\|^2$

Regression model in which the prediction is given by rounding to the closest label.

Feature extraction and supervised learning on fMRI:

from practice to theory

Fabian Pedregosa-Izquierdo, Parietal/Sierra (INRIA)

Study of cognitive function

Before the advent of non-invasive imaging modalities.

fMRI-based study

fMRI-based study

Feature extraction

Supervised Learning - Decoding

Predict stimuli from activation coefficients.

Outline

The General Linear Model (GLM)

Basis-constrained HRF

R1-GLM

Validation of R1-GLM

Results

Results - Encoding

Conclusions

Outline

Decoding with ordinal labels

X→y\mathbf{X} \quad \to \quad \mathbf{y}

Loss functions

Ordinal Logistic Regression

Pairwise ranking

Two fMRI datasets, three tasks

Results - Mean Absolute Error

Results - Pairwise Disagreement

Conclusions

Outline

Ordinal Regression surrogates

Empirical comparison

Fisher consistency

Illustration

Binary-class linear problem on R2\RR^2

Fisher consistency

Threshold-based surrogates

Consistency of ψℓ\psi^{\ell}

Illustration

Other results

Contributions

Perspectives

computational cost of R1-GLM

Perspectives

Consistency in a constrained space.

Thanks for your attention

Backup slides

The Linear-Time-Invariant assumption

HRF variability

Extension to separate designs

Results - Encoding

Results - Decoding

Absolute Error

$\mathbf{X} \quad \to \quad \mathbf{y}$

Binary-class linear problem on $\RR^2$

Consistency of $\psi^{\ell}$