Locally linear embedding and sparse eigensolvers
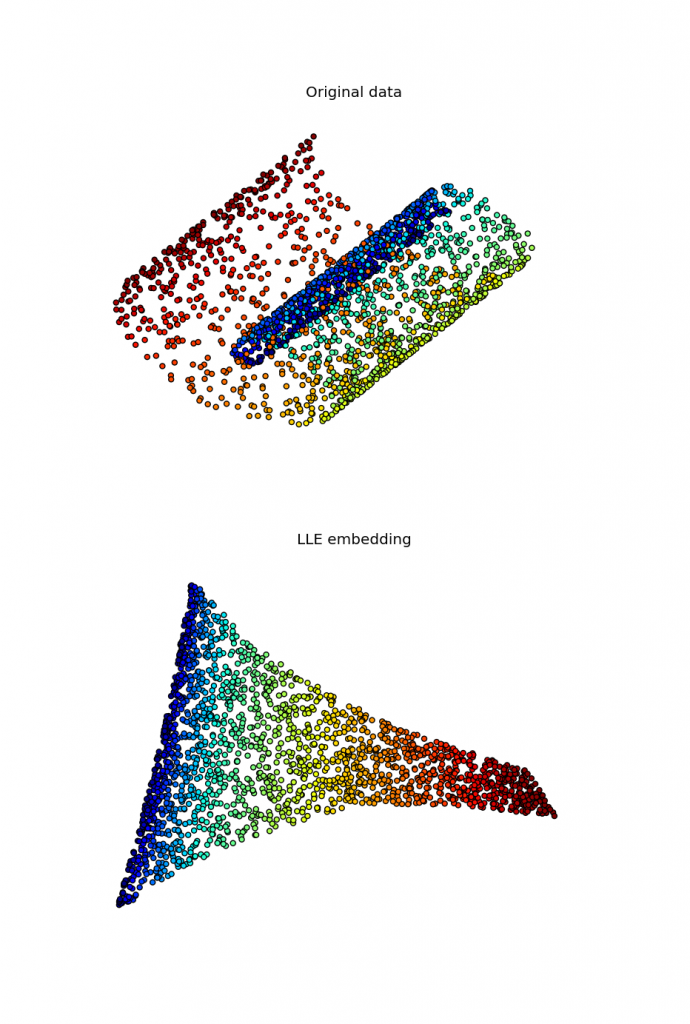
I've been working for some time on implementing a locally linear embedding algorithm for the upcoming manifold module in scikit-learn. While several implementations of this algorithm exist in Python, as far as I know none of them is able to use a sparse eigensolver in the last step of the algorithm, falling back to dense routines causing a huge overhead in this step. To overcome this, my first implementation used scipy.sparse.linalg.eigsh, which is a sparse eigensolver shipped by scipy and based on ARPACK. However, this approach converged extremely slowly, with timings that exceeded largely those of dense solvers. Recently I found a way that seems to work reasonably well, with timings that win by a factor of 5 on the swiss roll existing routines. This code is able to solve the problem making use of a preconditioner computed by PyAMG.
import numpy as np
from scipy.sparse import linalg, eye
from pyamg import smoothed_aggregation_solver
from scikits.learn import neighbors
def locally_linear_embedding(X, n_neighbors, out_dim, tol=1e-6, max_iter=200):
W = neighbors.kneighbors_graph(X, n_neighbors=n_neighbors, mode='barycenter') # M = (I-W)' (I-W)
A = eye(*W.shape, format=W.format) - W
A = (A.T).dot(A).tocsr() # initial approximation to the eigenvectors X = np.random.rand(W.shape[0], out\_dim)
ml = smoothed\_aggregation\_solver(A, symmetry='symmetric')
prec = ml.aspreconditioner() # compute eigenvalues and eigenvectors with LOBPCG
eigen\_values, eigen\_vectors = linalg.lobpcg( A, X, M=prec, largest=False, tol=tol, maxiter=max\_iter)
index = np.argsort(eigen\_values)
return eigen\_vectors[:, index], np.sum(eigen\_values) [/cc]
Full code for this algorithm applied to the swiss roll can be found here here, and I hope it will soon be part of scikit-learn.