Hyperparameter optimization with approximate gradient
TL;DR: I describe a method for hyperparameter optimization by gradient descent.
Most machine learning models rely on at least one hyperparameter to control for model complexity. For example, logistic regression commonly relies on a regularization parameter that controls the amount of $\ell_2$ regularization. Similarly, kernel methods also have hyperparameters that control for properties of the kernel, such as the "width" parameter in the RBF kernel. The fundamental distinction between model parameters and hyperparameters is that, while model parameters are estimated by minimizing a goodness of fit with the training data, hyperparameters need to be estimated by other means (such as a cross-validation loss), as otherwise models with excessive would be selected, a phenomenon known as overfitting.
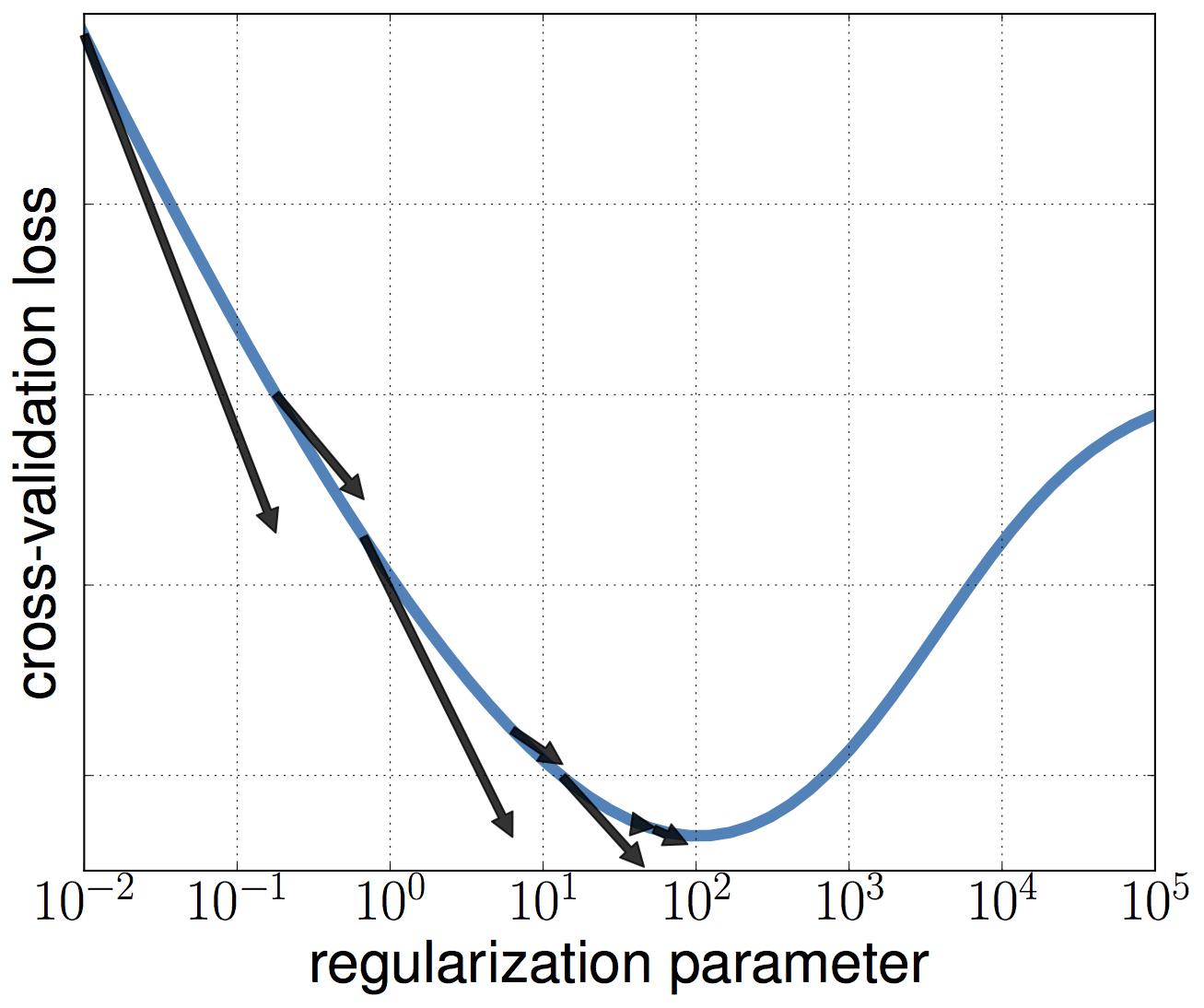 We can use an approximate gradient to optimize a cross-validation loss with respect to hyperparameters. A decreasing bound between the true gradient and the approximate gradient ensures that the method converges towards a local minima.
We can use an approximate gradient to optimize a cross-validation loss with respect to hyperparameters. A decreasing bound between the true gradient and the approximate gradient ensures that the method converges towards a local minima.
Fitting hyperparameters is essential to obtain models with good accuracy and computationally challenging. The existing most popular methods for fitting hyperparameters are based on either exhaustively exploring the whole hyperparameter space (grid search and random search) or on Bayesian optimization techniques that use previous function evaluations to guide the optimization procedure. The starting point of this work was a simple question: why are the procedures to estimate parameters and hyperparameters so different? Is it possible to use known and reliable methods such as gradient descent to fit not only parameters, but also hyperparameters?
Interestingly, I found out that this question had been answered a long time ago. Already in the 90s, Larsen et al. devised a method (described here and here) using gradient-descent to estimate the optimal value of $\ell_2$ regularization for neural networks. Shortly after, Y. Bengio also published a paper on this topic. Recently, there has been a renewed interest in gradient-based methods (see for example this paper by Maclaurin or a slightly earlier work by Justin Domke, and references therein).
One of the drawbacks of gradient-based optimization of hyperparameters, is that these depend on quantities that are costly to compute such as the exact value of the model parameters and the inverse of a Hessian matrix. The aim of this work is to relax some of these assumptions and provide a method that works when the quantities involved (such as model parameters) are known only approximately. In practice, what this means is that hyperparameters can be updated before model parameters have fully converged, which results in big computational gains. For more details and experiments, please take a look at the paper.
This paper was presented at the International Conference on Machine Learning (ICML 2016).Code is now available in github and these are the slides I used for the occasion:
Reviews
The original ICML reviews for this paper can be seen here and the rebuttal here. These were high quality reviews that had some rightful concerns with the first version of the manuscript. In fact, 2 out of 3 reviewers gave a "weak reject" in this first phase. Luckily these concerns could be contested in the rebuttal (the final manuscript was updated accordingly) and the 2 reviewers that gave a "weak reject" changed their rating to "weak accept" and the paper was finally accepted.
(Relatively) Frequently Asked Questions
- The outer loss function does not depend directly on the regularization parameter $\lambda$. Why is it there?
When the outer loss is a cross-validation loss this is indeed the case, but other criteria might depend on this parameter, such as the SURE criteria (see e.g. Deladalle et al. 2014).
Citing
Please cite this work if the paper or its associated code are relevant for you. You can use the following bibtex:
@inproceedings{PedregosaHyperparameter16,
author = {Fabian Pedregosa},
title = {Hyperparameter optimization with approximate gradient},
booktitle = {Proceedings of the 33nd International Conference on Machine Learning ({ICML})},
year = {2016},
url = {http://proceedings.mlr.press/v48/pedregosa16.html},
}
Erratum
An early version of the paper contained the following typo: the first equation in Theorem 2 should read $\sum_{i=1}^\infty \varepsilon_i \lt \infty$ instead of $\sum_{i=1}^\infty \varepsilon_i \leq \infty$ (note the $<$ in the first equation versus $\leq$ in the second one). This typo has been corrected in both ArXiv version and the proceedings.