Following a challenge proposed by Gael to my
group I compared several implementations of
Logistic Regression. The task was to implement a Logistic Regression model
using standard optimization tools from scipy.optimize and compare
them against state of the art implementations such as
LIBLINEAR.
In this blog post I'll write down all the implementation details of this
model, in the hope that not only the conclusions but also the process would be
useful for future comparisons and benchmarks.
Function evaluation
The loss function for the $\ell_2$-regularized logistic regression, i.e. the
function to be minimized is
$$
\mathcal{L}(w, \lambda, X, y) = - \sum_{i=1}^n \log(\phi(y_i w^T X_i)) + \lambda w^T w
$$
where $\phi(t) = 1. / (1 + \exp(-t))$ is the logistic
function, $\lambda w^T w$ is
the regularization term and $X, y$ is the input data, with $X \in
\mathbb{R}^{n \times p}$ and $y \in \{-1, 1\}^n$. However, this formulation is
not great from a practical standpoint. Even for not unlikely values of $t$
such as $t = -100$, $\exp(100)$ will overflow, assigning the loss an
(erroneous) value of $+\infty$. For this reason , we evaluate
$\log(\phi(t))$ as
$$
\log(\phi(t)) =
\begin{cases}
- \log(1 + \exp(-t)) \text{ if } t > 0 \\
t - \log(1 + \exp(t)) \text{ if } t \leq 0\\
\end{cases}
$$
The gradient of the loss function is given by
$$
\nabla_w \mathcal{L} = \sum_{i=1}^n y_i X_i (\phi(y_i w^T X_i) - 1) + \lambda w
$$
Similarly, the logistic function $\phi$ used here can be computed in a more
stable way using the formula
$$
\phi(t) = \begin{cases}
1 / (1 + \exp(-t)) \text{ if } t > 0 \\
\exp(t) / (1 + \exp(t)) \text{ if } t \leq 0\\
\end{cases}
$$
Finally, we will also need the Hessian for some second-order methods, which is given by
$$
\nabla_w ^2 \mathcal{L} = X^T D X + \lambda I
$$
where $I$ is the identity matrix and $D$ is a diagonal matrix given by $D_{ii} = \phi(y_i w^T X_i)(1 - \phi(y_i w^T X_i))$.
In Python, these function can be written as
def phi(t):
# logistic function, returns 1 / (1 + exp(-t))
idx = t > 0
out = np.empty(t.size, dtype=np.float)
out[idx] = 1. / (1 + np.exp(-t[idx]))
exp_t = np.exp(t[~idx])
out[~idx] = exp_t / (1. + exp_t)
return out
def loss(w, X, y, alpha):
# logistic loss function, returns Sum{-log(phi(t))}
z = X.dot(w)
yz = y * z
idx = yz > 0
out = np.zeros_like(yz)
out[idx] = np.log(1 + np.exp(-yz[idx]))
out[~idx] = (-yz[~idx] + np.log(1 + np.exp(yz[~idx])))
out = out.sum() + .5 * alpha * w.dot(w)
return out
def gradient(w, X, y, alpha):
# gradient of the logistic loss
z = X.dot(w)
z = phi(y * z)
z0 = (z - 1) * y
grad = X.T.dot(z0) + alpha * w
return grad
def hessian(s, w, X, y, alpha):
# hessian of the logistic loss
z = X.dot(w)
z = phi(y * z)
d = z * (1 - z)
wa = d * X.dot(s)
Hs = X.T.dot(wa)
out = Hs + alpha * s
return out
Benchmarks
I tried several methods to estimate this $\ell_2$-regularized logistic regression. There is
one first-order method (that is, it only makes use of the gradient and not of
the Hessian), Conjugate
Gradient
whereas all the others are Quasi-Newton methods. The method I tested are:
- CG = Conjugate Gradient as implemented in
scipy.optimize.fmin_cg
- TNC = Truncated Newton as implemented in
scipy.optimize.fmin_tnc
- BFGS = Broyden–Fletcher–Goldfarb–Shanno method, as implemented in
scipy.optimize.fmin_bfgs.
- L-BFGS = Limited-memory BFGS as implemented in
scipy.optimize.fmin_l_bfgs_b. Contrary to the BFGS algorithm, which is written in Python, this one wraps a C implementation.
- Trust Region = Trust Region Newton method . This is the solver used by LIBLINEAR that I've wrapped to accept any Python function in the package pytron
To assure the most accurate results across implementations, all timings were
collected by callback functions that were called from the algorithm on each
iteration. Finally, I plot the maximum absolute value of the gradient (=the
infinity norm of the gradient) with respect to time.
The synthetic data used in the benchmarks was generated as described in and consists
primarily of the design matrix $X$ being Gaussian noise, the vector of
coefficients is drawn also from a Gaussian distribution and the explained
variable $y$ is generated as $y = \text{sign}(X w)$. We then perturb matrix
$X$ by adding Gaussian noise with covariance 0.8. The number of samples and features
was fixed to $10^4$ and $10^3$ respectively. The penalization parameter $\lambda$ was
fixed to 1.
In this setting variables are typically uncorrelated and most solvers perform
decently:
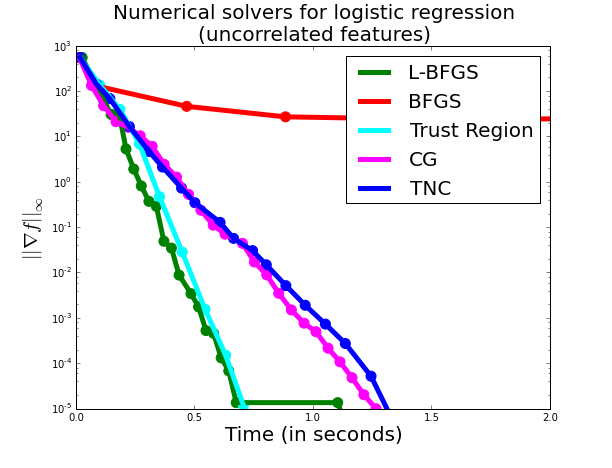
Here, the Trust Region and L-BFGS solver perform almost equally good, with
Conjugate Gradient and Truncated Newton falling shortly behind. I was surprised
by the difference between BFGS and L-BFGS, I would have thought that when memory was not an issue both algorithms should perform similarly.
To make things more interesting, we now make the design to be slightly more
correlated. We do so by adding a constant term of 1 to the matrix $X$ and
adding also a column vector of ones this matrix to account for the intercept. These are the results:
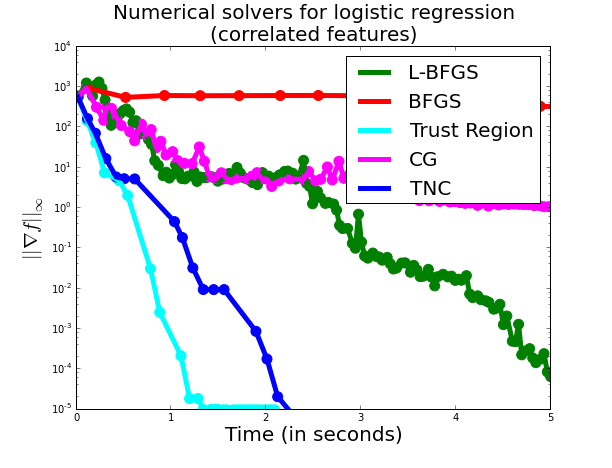
Here, we already see that second-order methods dominate over first-order
methods (well, except for BFGS), with Trust Region clearly dominating the
picture but with TNC not far behind.
Finally, if we force the matrix to be even more correlated (we add 10. to the
design matrix $X$), then we have:
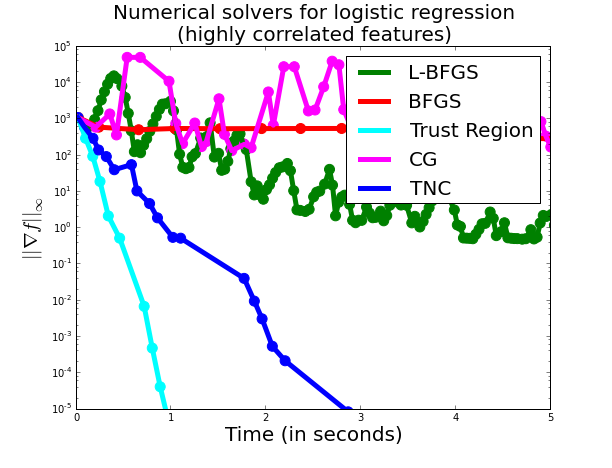
Here, the Trust-Region method has the same timing as before, but all other
methods have got substantially worse.The Trust Region
method, unlike the other methods is surprisingly robust to correlated designs.
To sum up, the Trust Region method performs extremely well for optimizing the
Logistic Regression model under different conditionings of the design matrix.
The LIBLINEAR software uses
this solver and thus has similar performance, with the sole exception that the
evaluation of the logistic function and its derivatives is done in C++ instead
of Python. In practice, however, due to the small number of iterations of this
solver I haven't seen any significant difference.
There are comments.