Announce: first public release of lightning!, a library for large-scale linear classification, regression and ranking in Python. The library was started a couple of years ago by Mathieu Blondel who also contributed the vast majority of source code. I joined recently its development and decided it was about time for …
Together with other scikit-learn developers we've created an umbrella organization for scikit-learn-related projects named scikit-learn-contrib. The idea is for this organization to host projects that are deemed too specific or too experimental to be included in the scikit-learn codebase but still offer an API which is compatible with scikit-learn and …
Recently I've implemented, together with Arnaud Rachez, the SAGA[] algorithm in the lightning machine learning library (which by the way, has been recently moved to the new scikit-learn-contrib project). The lightning library uses the same API as scikit-learn but is particularly adapted to online learning. As for the SAGA …
Cross-validation iterators in scikit-learn are simply generator objects, that is, Python objects that implement the __iter__ method and that for each call to this method return (or more precisely, yield) the indices or a boolean mask for the train and test set. Hence, implementing new cross-validation iterators that behave as …
Due to lack of time and interest, I'm no longer maintaining this project. Feel free to grab the sources from https://github.com/fabianp/nbgallery and fork the project.
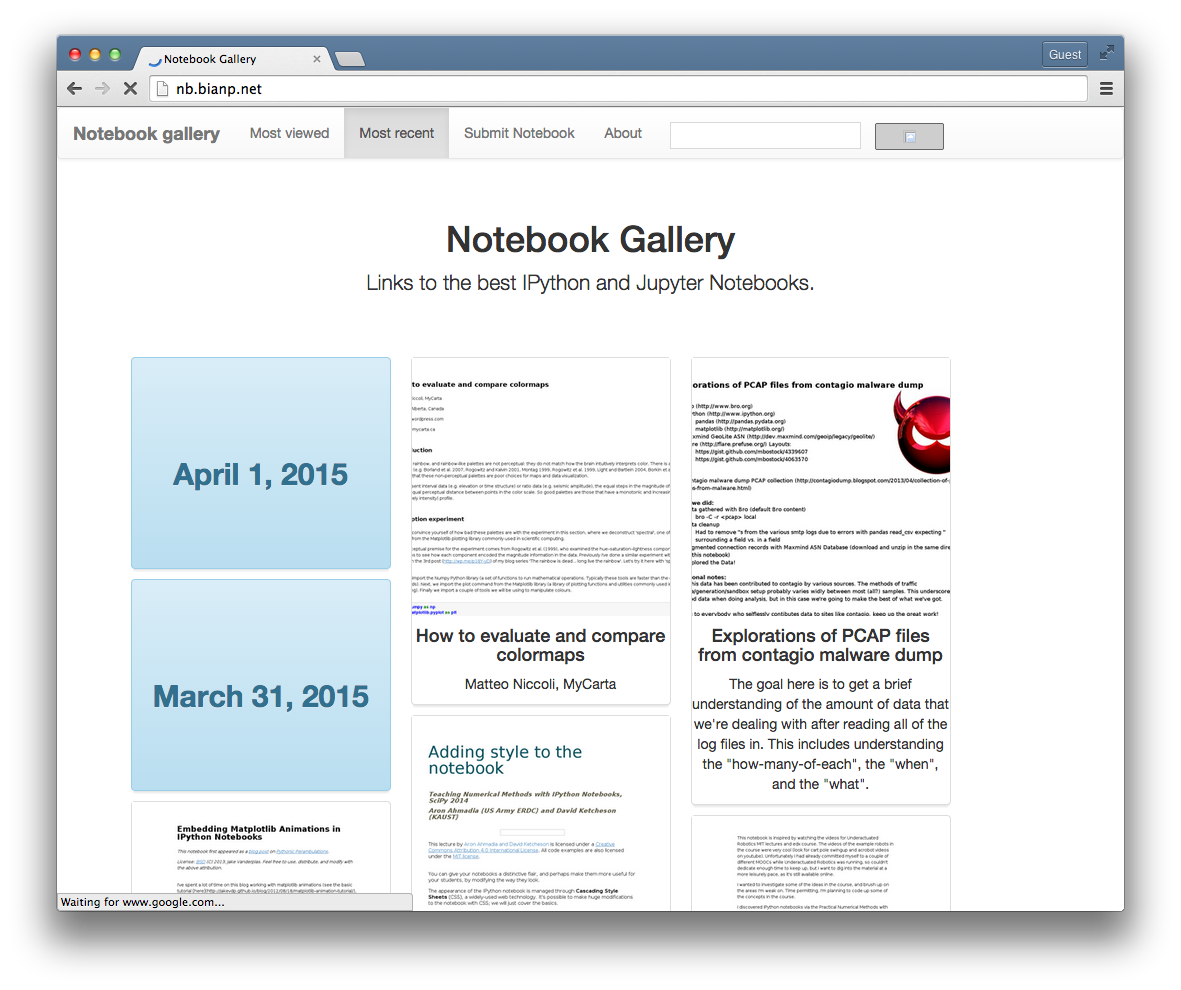
TL;DR I created a gallery for IPython/Jupyter notebooks. Check it out :-)
A couple of months ago I put online …
Last Friday was PyData Paris, in words of the organizers, ''a gathering of users and developers of data analysis tools in Python''.

The organizers did a great job in putting together and the event started already with a full room for Gael's keynote
My take-away message from the talks is …
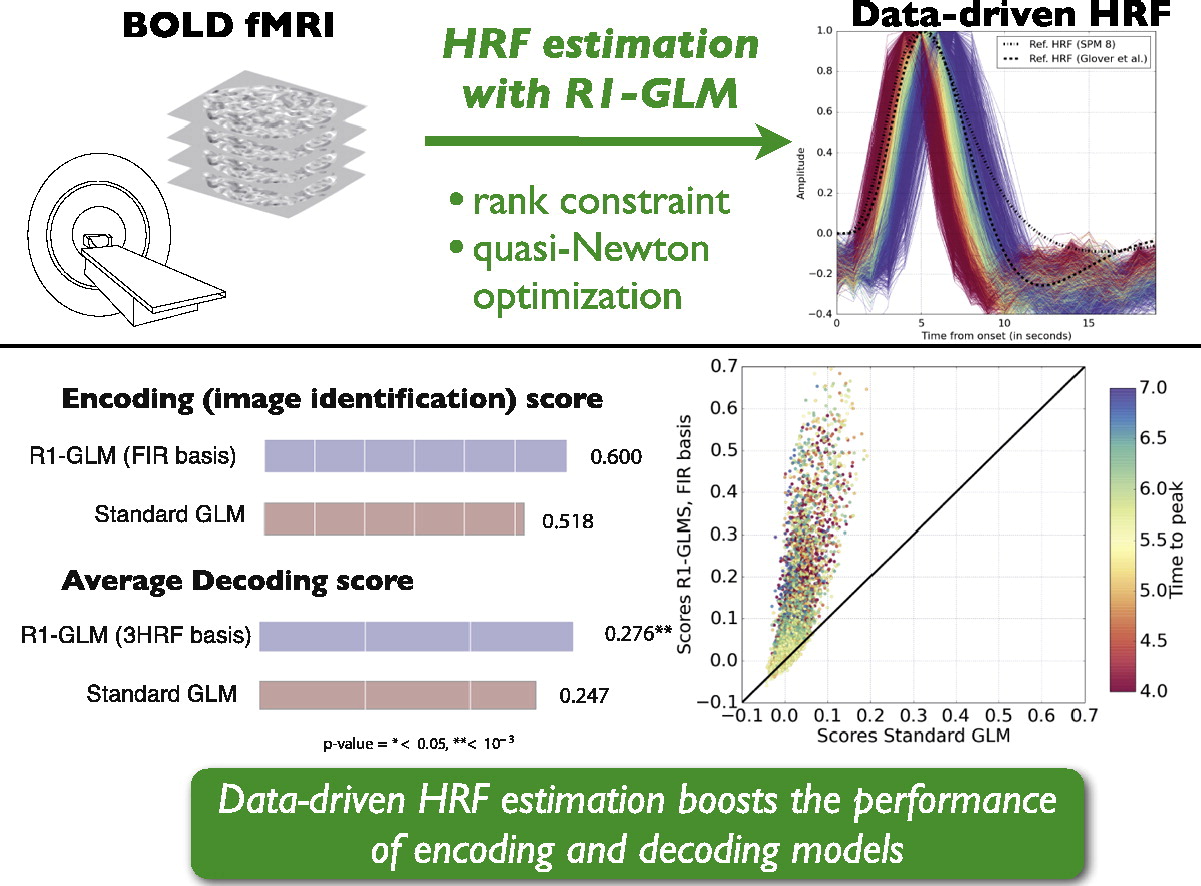
My latest research paper[] deals with the estimation of the hemodynamic response function (HRF) from fMRI data.
This is an important topic since the knowledge of a hemodynamic response function is what makes it possible to extract the brain activation maps that are used in most of the impressive …
As part of the development of
memory_profiler I've tried
several ways to get memory usage of a program from within Python. In this post
I'll describe the different alternatives I've tested.
The psutil library
psutil is a python library that provides
an interface for retrieving information on running processes. It …
In this post I compar several implementations of
Logistic Regression. The task was to implement a Logistic Regression model
using standard optimization …
TL;DR: I've implemented a logistic ordinal regression or
proportional odds model. Here is the Python code
The logistic ordinal regression model …
My latest contribution for scikit-learn is
an implementation of the isotonic regression model that I coded with
Nelle Varoquaux and
Alexandre Gramfort …
Besides performing a line-by-line analysis of memory consumption,
memory_profiler
exposes some functions that allow to retrieve the memory consumption
of a function in real-time, allowing e.g. to visualize the memory
consumption of a given function over time.
The function to be used is memory_usage. The first argument
specifies what …
SciPy contains two methods to compute the singular value decomposition (SVD) of a matrix: scipy.linalg.svd and scipy.sparse.linalg.svds. In this post I'll compare both methods for the task of computing the full SVD of a large dense matrix.
The first method, scipy.linalg.svd, is perhaps …
This tutorial introduces the concept of pairwise preference used in most ranking problems. I'll use scikit-learn and for learning and matplotlib for …
My newest project is a Python library for monitoring memory consumption
of arbitrary process, and one of its most useful features is the
line-by-line analysis of memory usage for Python code. I wrote a basic
prototype six months ago after being surprised by the lack of related
tools. I wanted …
A little experiment to see what low rank approximation looks like. These
are the best rank-k approximations (in the Frobenius norm) to the a
natural image for increasing values of k and an original image of rank
512.

Python code can be found here. GIF animation made
using ImageMagic's convert …
In scipy's development version there's a new function closely related to
the QR-decomposition of a matrix and to the least-squares solution of
a linear system. What this function does is to compute the
QR-decomposition of a matrix and then multiply the resulting orthogonal
factor by another arbitrary matrix. In pseudocode …
As a warm-up for the upcoming EuroScipy-conference, some of the
scikit-learn developers decided to gather and work together for a
couple of days. Today was the first day and there was only a handfull of
us, as the real kickoff is expected tomorrow. Some interesting coding
happened, although most of …
I was last weekend in FOSDEM presenting scikits.learn (here are
the slides I used at the Data Analytics Devroom). Kudos to Olivier
Grisel and all the people who organized such a fun and authentic
meeting!