** Note: this post contains a fair amount of LaTeX, if you don't visualize the math correctly come to its original location **

In machine learning it is common to formulate the classification task as a minimization problem over a given loss function. Given data input data $(x_1, ..., x_n)$ and associated labels $(y_1, ..., y_n), y_i \in \lbrace-1, 1\rbrace$, the problem becomes to find a function $f(x)$ that minimizes

$$L(x, y) = \sum_i ^n \text{loss}(f(x_i), y_i)$$

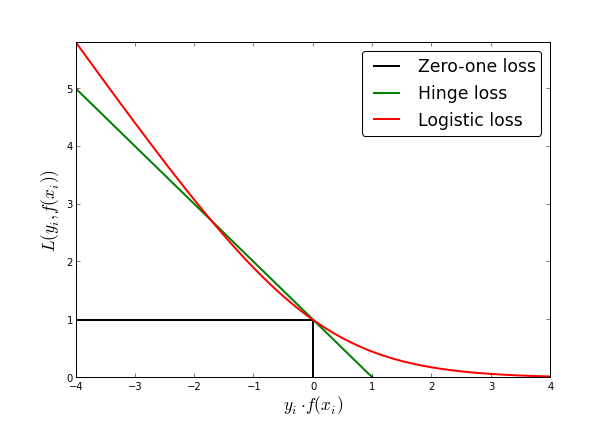
where loss is any loss function. These are usually functions that become close to zero when $f(x_i)$ agrees in sign with $y_i$ and have a non-negative value when $f(x_i)$ have opposite signs. Common choices of loss functions are:

• Zero-one loss, $I(f(x_i) = y_i)$, where $I$ is the indicator function.
• Hinge loss, $\text{max}(0, 1 - f(x_i) y_i)$
• Logistic loss, $\log(1 + \exp{f(x_i) y_i})$

¹

In the paper Loss functions for preference levels: Regression with discrete ordered labels, the above setting that is commonly used in the classification and regression setting is extended for the ordinal regression problem. In ordinal regression, classes can take one of several discrete, but ordered, labels. Think for example on movie ratings that go from zero to ten stars. Here there's an inherent order in the sense that (unlike the multiclass classification setting) not all errors are equally bad. For instance, it is worse to mistake a 1-star with a 10-star than a 4-star movie with a 5-star one.

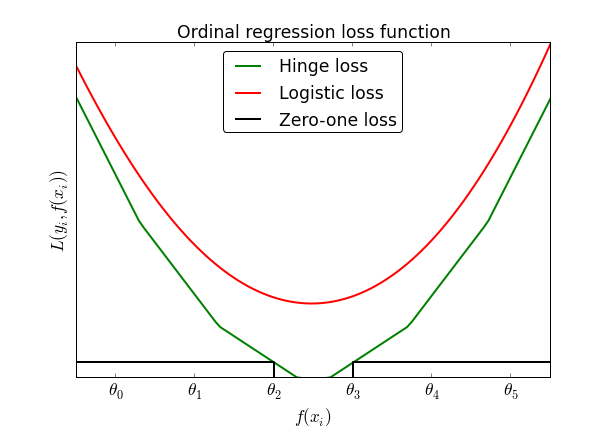
To extend the binary loss to the case of ordinal regression, the author introduces K-1 thresholds $-\infty = \theta_0 \lt \theta_1 \lt ... \lt \theta_{K-1}=\infty$. Each of the K segments corresponds to one of K labels and a predicted value between $\theta_{d}$ and $\theta_{d+1}$ corresponds to the prediction of class $d$ (supposing that classes to from zero to $d$). This generalizes the binary case by considering zero the unique threshold.

Suppose K=7 and a that the correct outcome of $y_i$ is 2, that is, $f(x_i)$ must lie between $\theta_1$ and $\theta_2$. In that case, it must be verified that $f(x_i) > \theta_0$ and $f(x_i) > \theta_1$ as well as $f(x_i) < \theta_3 < \theta_4 < \theta_5$. Treating this as K-1=6 independent classification problems produces the following family of loss functions (for a hinge loss):

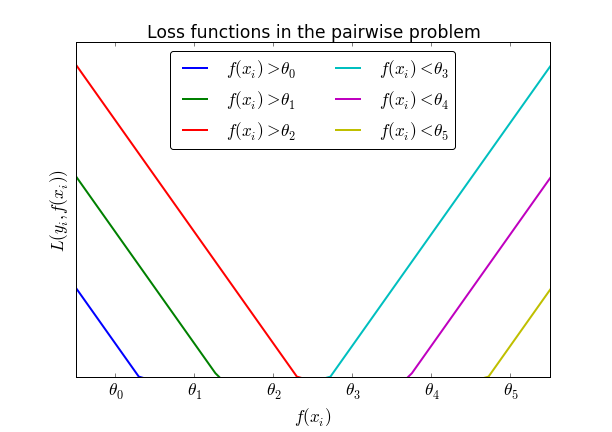
The idea behind Rennie's paper is to sum all these loss function to produce a single optimization problem that is then the sum of all threshold violations. Here, not only the function increases when thresholds are violated, but the slope of the loss function increases each time a threshold is crossed.