Performance of our AI system relative to human competitors at IMO 2024. We earned 28 out of 42 total points, achieving the same level as a silver medalist in the competition.
Here are my most recent publications in reverse chronological order. A similar list can also be found in my Google Scholar profile.
Performance of our AI system relative to human competitors at IMO 2024. We earned 28 out of 42 total points, achieving the same level as a silver medalist in the competition.
AI achieves silver-medal standard solving International Mathematical Olympiad problems, AlphaProof and AlphaGeometry teams
Abstract: AlphaProof is a new reinforcement-learning-based system for formal math reasoning, and AlphaGeometry 2 is an improved version of our geometry-solving system. Together, these systems solved four out of six problems from this year’s International Mathematical Olympiad (IMO), achieving the same level as a silver medalist in the competition for the first time.
Stepping on the Edge: Curvature Aware Learning Rate Tuners , Vincent Roulet, Atish Agarwala, Jean-Bastien Grill, Grzegorz Swirszcz, Mathieu Blondel, Fabian Pedregosa. [ArXiv],
Abstract: Curvature information -- particularly, the largest eigenvalue of the loss Hessian, known as the sharpness -- often forms the basis for learning rate tuners. However, recent work has shown that the curvature information undergoes complex dynamics during training, going from a phase of increasing sharpness to eventual stabilization. We analyze the closed-loop feedback effect between learning rate tuning and curvature. We find that classical learning rate tuners may yield greater one-step loss reduction, yet they ultimately underperform in the long term when compared to constant learning rates in the full batch regime. These models break the stabilization of the sharpness, which we explain using a simplified model of the joint dynamics of the learning rate and the curvature. To further investigate these effects, we introduce a new learning rate tuning method, Curvature Dynamics Aware Tuning (CDAT), which prioritizes long term curvature stabilization over instantaneous progress on the objective. In the full batch regime, CDAT shows behavior akin to prefixed warm-up schedules on deep learning objectives, outperforming tuned constant learning rates. In the mini batch regime, we observe that stochasticity introduces confounding effects that explain the previous success of some learning rate tuners at appropriate batch sizes. Our findings highlight the critical role of understanding the joint dynamics of the learning rate and curvature, beyond greedy minimization, to diagnose failures and design effective adaptive learning rate tuners.
On the Interplay Between Stepsize Tuning and Progressive Sharpening, Vincent Roulet, Atish Agarwala, Fabian Pedregosa, OPT2023. [ArXiv],
Abstract: Recent empirical work has revealed an intriguing property of deep learning models by which the sharpness (largest eigenvalue of the Hessian) increases throughout optimization until it stabilizes around a critical value at which the optimizer operates at the edge of stability, given a fixed stepsize (Cohen et al, 2022). We investigate empirically how the sharpness evolves when using stepsize-tuners, the Armijo linesearch and Polyak stepsizes, that adapt the stepsize along the iterations to local quantities such as, implicitly, the sharpness itself. We find that the surprisingly poor performance of a classical Armijo linesearch may be well explained by its tendency to ever-increase the sharpness of the objective in the full or large batch regimes. On the other hand, we observe that Polyak stepsizes operate generally at the edge of stability or even slightly beyond, while outperforming its Armijo and constant stepsizes counterparts. We conclude with an analysis that suggests unlocking stepsize tuners requires an understanding of the joint dynamics of the step size and the sharpness.
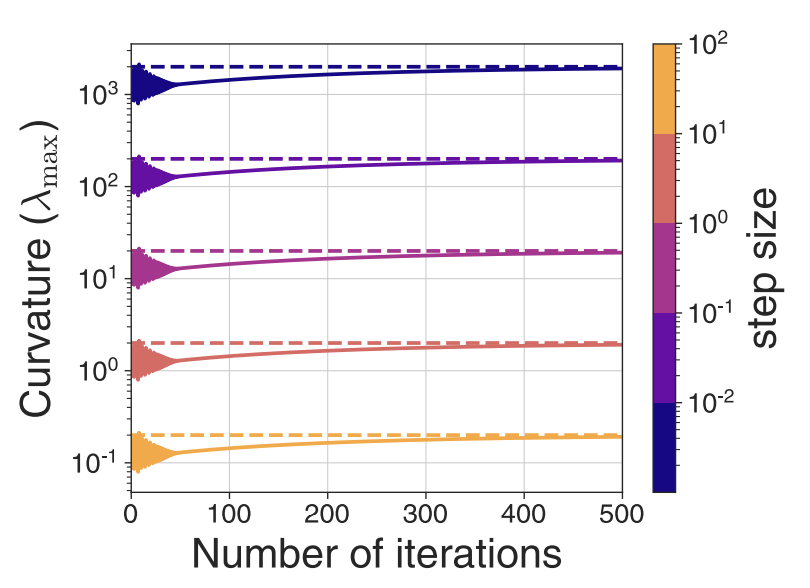
We develop a simple model where the objective function is quartic in the parameters that exhibits progressive sharpening.
Second-order regression models exhibit progressive sharpening to the edge of stability, Atish Agarwala, Fabian Pedregosa, Jeffrey Pennington, International Conference on Machine Learning. [ArXiv], [Poster]
Abstract: Recent studies of gradient descent with large step sizes have shown that there is often a regime with an initial increase in the largest eigenvalue of the loss Hessian (progressive sharpening), followed by a stabilization of the eigenvalue near the maximum value which allows convergence (edge of stability). These phenomena are intrinsically non-linear and do not happen for models in the constant Neural Tangent Kernel (NTK) regime, for which the predictive function is approximately linear in the parameters. As such, we consider the next simplest class of predictive models, namely those that are quadratic in the parameters, which we call second-order regression models. For quadratic objectives in two dimensions, we prove that this second-order regression model exhibits progressive sharpening of the NTK eigenvalue towards a value that differs slightly from the edge of stability, which we explicitly compute. In higher dimensions, the model generically shows similar behavior, even without the specific structure of a neural network, suggesting that progressive sharpening and edge-of-stability behavior aren't unique features of neural networks, and could be a more general property of discrete learning algorithms in high-dimensional non-linear models.
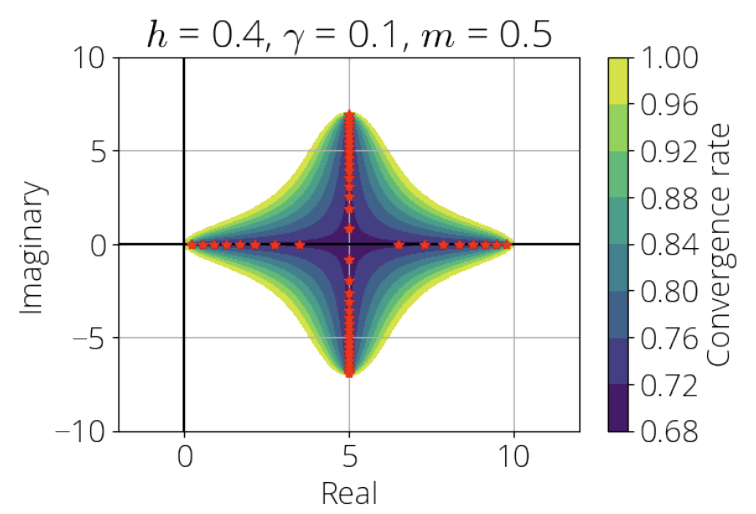
For some choice of parameters, extragradient converges for problems where the Jacobian's eigenvalues are in the dark region above.
Extragradient with Positive Momentum is Optimal for Games with Cross-Shaped Jacobian Spectrum, Junhyung Lyle Kim, Gauthier Gidel, Anastasios Kyrillidis, Fabian Pedregosa, preprint, 2022. [ArXiv]
Abstract: The extragradient method has recently gained increasing attention, due to its convergence behavior on smooth games. In n-player differentiable games, the eigenvalues of the Jacobian of the vector field are distributed on the complex plane, exhibiting more convoluted dynamics compared to classical (i.e., single player) minimization. In this work, we take a polynomial-based analysis of the extragradient with momentum for optimizing games with cross-shaped Jacobian spectrum on the complex plane. We show two results. First, based on the hyperparameter setup, the extragradient with momentum exhibits three different modes of convergence: when the eigenvalues are distributed i) on the real line, ii) both on the real line along with complex conjugates, and iii) only as complex conjugates. Then, we focus on the case ii), i.e., when the eigenvalues of the Jacobian have cross-shaped structure, as observed in training generative adversarial networks. For this problem class, we derive the optimal hyperparameters of the momentum extragradient method, and show that it achieves an accelerated convergence rate.
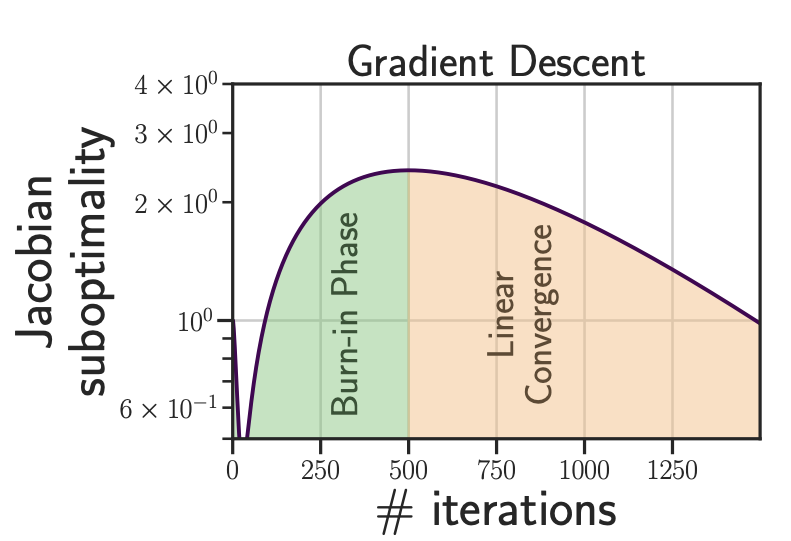
Gradient descent exhibit two distinct
phases during unrolled differentiation: an initial burn-in phase, where the Jacobian suboptimality increases, followed by a convergent phase with an asymptotic linear convergence.
The Curse of Unrolling: Rate of Differentiating Through Optimization, Damien Scieur, Quentin Bertrand, Gauthier Gidel, Fabian Pedregosa, Advances in Neural Information Processing Systems 35, 2022. [ArXiv]
Abstract: Computing the Jacobian of the solution of an optimization problem is a central problem in machine learning, with applications in hyperparameter optimization, meta-learning, optimization as a layer, and dataset distillation, to name a few. Unrolled differentiation is a popular heuristic that approximates the solution using an iterative solver and differentiates it through the computational path. This work provides a non-asymptotic convergence-rate analysis of this approach on quadratic objectives for gradient descent and the Chebyshev method. We show that to ensure convergence of the Jacobian, we can either 1) choose a large learning rate leading to a fast asymptotic convergence but accept that the algorithm may have an arbitrarily long burn-in phase or 2) choose a smaller learning rate leading to an immediate but slower convergence. We refer to this phenomenon as the curse of unrolling. Finally, we discuss open problems relative to this approach, such as deriving a practical update rule for the optimal unrolling strategy and making novel connections with the field of Sobolev orthogonal polynomials.
JAXopt makes it easy to solve complicated bi-level problems such as dataset distillation. Above, an example of this problem where the model finds the best 10 images such that a linear model trained on these images gives the best generalization accuracy on MNIST.
Efficient and Modular Implicit Differentiation, Mathieu Blondel, Quentin Berthet, Marco Cuturi, Roy Frostig, Stephan Hoyer, Felipe Llinares-López, Fabian Pedregosa, Jean-Philippe Vert, Advances in Neural Information Processing Systems 35, 2022. [ArXiv], [Slides], [Code].
Abstract: We propose a unified, efficient and modular approach for implicit differentiation of optimization problems. In our approach, the user defines (in Python in the case of our implementation) a function F capturing the optimality conditions of the problem to be differentiated. Once this is done, we leverage autodiff of F and implicit differentiation to automatically differentiate the optimization problem. Our approach thus combines the benefits of implicit differentiation and autodiff. It is efficient as it can be added on top of any state-of-the-art solver and modular as the optimality condition specification is decoupled from the implicit differentiation mechanism. We show that seemingly simple principles allow to recover many recently proposed implicit differentiation methods and create new ones easily. We demonstrate the ease of formulating and solving bi-level optimization problems using our framework. We also showcase an application to the sensitivity analysis of molecular dynamics.
Decision boundary of a dataset distillation problem across iterations.
On Implicit Bias in Overparameterized Bilevel Optimization, Paul Vicol, Jonathan P Lorraine, Fabian Pedregosa, David Duvenaud, Roger B Grosse, Proceedings of the 39th International Conference on Machine Learning, 2022. [PMLR]
Abstract: Many problems in machine learning involve bilevel optimization (BLO), including hyperparameter optimization, meta-learning, and dataset distillation. Bilevel problems involve inner and outer parameters, each optimized for its own objective. Often, at least one of the two levels is underspecified and there are multiple ways to choose among equivalent optima. Inspired by recent studies of the implicit bias induced by optimization algorithms in single-level optimization, we investigate the implicit bias of different gradient-based algorithms for jointly optimizing the inner and outer parameters. We delineate two standard BLO methods—cold-start and warm-start BLO—and show that the converged solution or long-run behavior depends to a large degree on these and other algorithmic choices, such as the hypergradient approximation. We also show that the solutions from warm-start BLO can encode a surprising amount of information about the outer objective, even when the outer optimization variables are low-dimensional. We believe that implicit bias deserves as central a role in the study of bilevel optimization as it has attained in the study of single-level neural net optimization.
Number of submissions across the years, color coded according to its editorial decision.
Retrospectives from 20 Years of JMLR, Fabian Pedregosa, Tegan Maharaj, Alp Kucukelbir, Rajarshi Das, Valentina Borghesani, Francis Bach, David Blei, Bernhard Schölkopf, 2022. [JMLR]
Abstract: In 2000, led by editor-in-chief Leslie Kaelbling, JMLR was founded as a fully free and open-access platform for publishing high-quality machine learning research. Twenty-one years later, JMLR publishes more than 250 papers per year and is one of the premiere publishing venues in the field of artificial intelligence. How did a community-driven journal, without any financial or managerial support from traditional publishing companies, become a leading journal in the field? Celebrating more than 20 years of history, we take a look back at the story of JMLR and the lessons that can be learnt from it.
Cutting Some Slack for SGD with Adaptive Polyak Stepsizes, Robert M. Gower, Mathieu Blondel, Nidham Gazagnadou, Fabian Pedregosa, under review , 2022. [ArXiv].
Abstract: Tuning the step size of stochastic gradient descent is tedious and error prone. This has motivated the development of methods that automatically adapt the step size using readily available information. In this paper, we consider the family of SPS (Stochastic gradient with a Polyak Stepsize) adaptive methods. These are methods that make use of gradient and loss value at the sampled points to adaptively adjust the step size. We first show that SPS and its recent variants can all be seen as extensions of the Passive-Aggressive methods applied to nonlinear problems. We use this insight to develop new variants of the SPS method that are better suited to nonlinear models. Our new variants are based on introducing a slack variable into the interpolation equations. This single slack variable tracks the loss function across iterations and is used in setting a stable step size. We provide extensive numerical results supporting our new methods and a convergence theory.
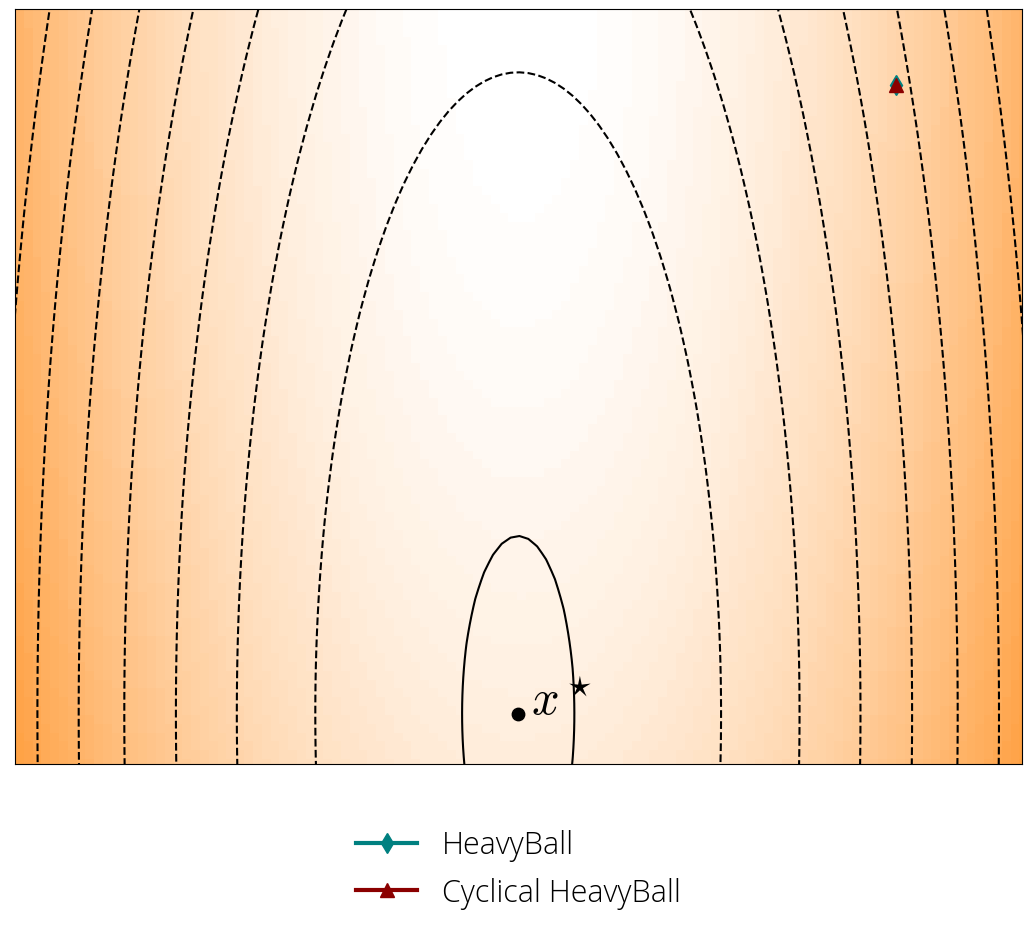
Under some assumptions on the Hessian eigenvalues, one can achieve faster convergence by alternating between two different step-sizes.
Super-Acceleration with Cyclical Step-sizes, Baptiste Goujaud, Damien Scieur, Aymeric Dieuleveut, Adrien Taylor, Fabian Pedregosa, Proceedings of the 25th International Conference on Artificial Intelligence and Statistics, 2022. [ArXiv], [Slides], [Video] [Blog post].
Abstract: We develop a convergence rate analysis for quadratic objectives that provides optimal parameters and shows that cyclical learning rates can improve upon traditional lower complexity bounds. We further propose a systematic approach to design optimal first order methods for quadratic minimization with a given spectral structure. Finally, we provide a local convergence rate analysis beyond quadratic minimization for the proposed methods and illustrate our findings through benchmarks on least squares and logistic regression problems.
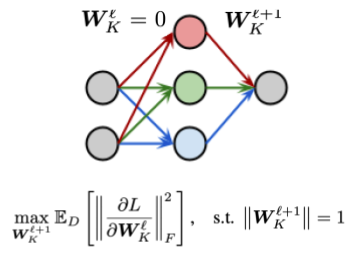
GradMax poses the problem of initializing new neurons as an eigenvalue problem.
GradMax: Growing Neural Networks using Gradient Information, Utku Evci, Max Vladymyrov, Thomas Unterthiner, Bart van Merriënboer, Fabian Pedregosa, Proceedings of the Tenth International Conference on Learning Representations, 2022. [ArXiv], [OpenReview].
Abstract: The architecture and the parameters of neural networks are often optimized independently, which requires costly retraining of the parameters whenever the architecture is modified. In this work we instead focus on growing the architecture without requiring costly retraining. We present a method that adds new neurons during training without impacting what is already learned, while improving the training dynamics. We do this by maximizing the gradients of the new neurons and find an approximation to the optimal initialization by means of the singular value decomposition (SVD). We call this technique Gradient Maximizing Growth (GradMax) and demonstrate its effectiveness in variety of vision tasks and architectures.
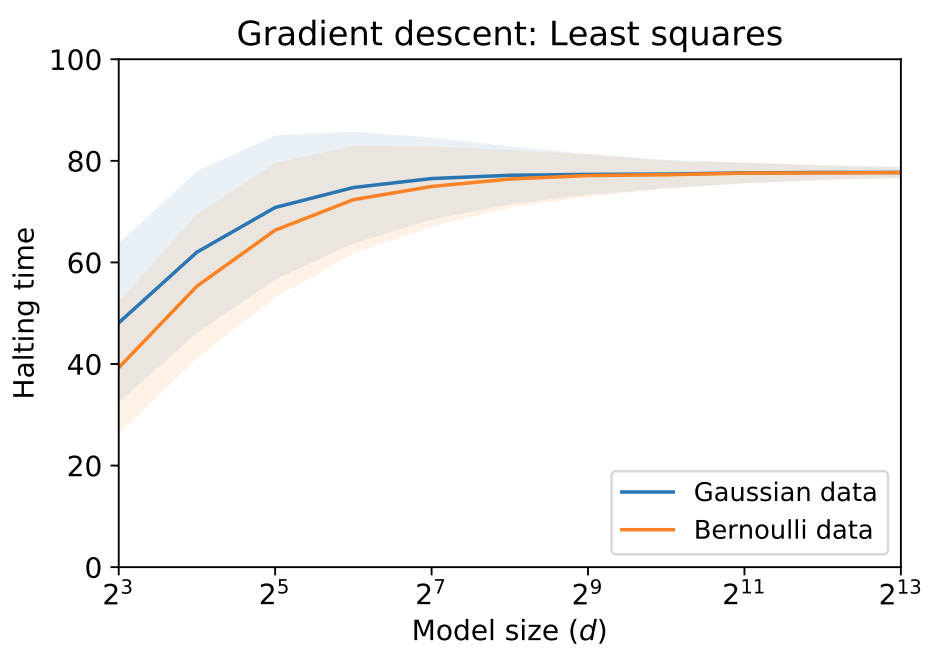
As the model grows (x-axis), the standard deviation (shaded region) in the halting time
of gradient descent on random least squares vanishes and the halting time becomes predictable.
Halting Time is Predictable for Large Models: A Universality Property and Average-case Analysis, Courtney Paquette, Bart van Merriënboer, Elliot Paquette, Fabian Pedregosa, Foundations of Computational Mathematics, 2022. [ArXiv], [Journal].
Abstract: Average-case analysis computes the complexity of an algorithm averaged over all possible inputs. Compared to worst-case analysis, it is more representative of the typical behavior of an algorithm, but remains largely unexplored in optimization. One difficulty is that the analysis can depend on the probability distribution of the inputs to the model. However, we show that this is not the case for a class of large-scale problems trained with gradient descent including random least squares and one-hidden layer neural networks with random weights. In fact, the halting time exhibits a universality property: it is independent of the probability distribution. With this barrier for average-case analysis removed, we provide the first explicit average-case convergence rates showing a tighter complexity not captured by traditional worst-case analysis. Finally, numerical simulations suggest this universality property holds for a more general class of algorithms and problems.
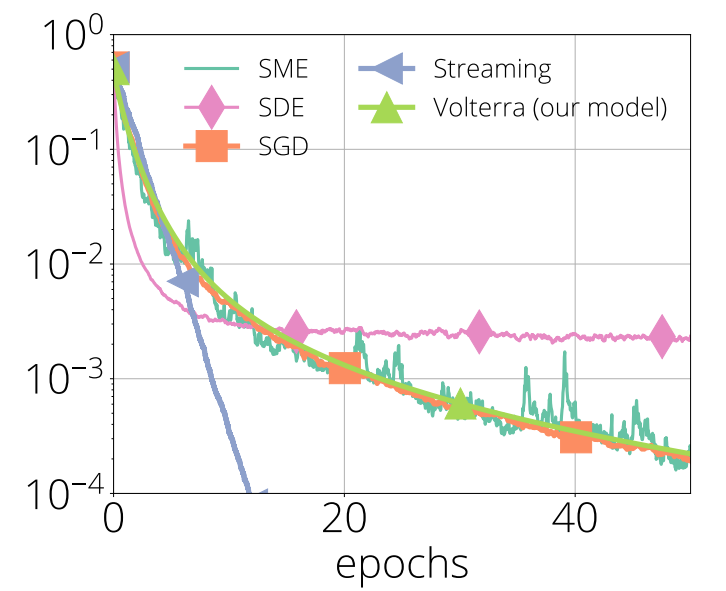
The Volterra equation model accurately tracks SGD on a random least-squares problem for any choice of stepsize. Other models introduce biases that substantially impact model fidelity.
SGD in the Large: Average-case Analysis, Asymptotics, and Stepsize Criticality, Courtney Paquette, Kiwon Lee, Fabian Pedregosa, Elliot Paquette, Conference on Learning Theory (COLT), 2021. [ArXiv], [Video], [Proceedings].
Abstract: We propose a new framework, inspired by random matrix theory, for analyzing the dynamics of stochastic gradient descent (SGD) when both number of samples and dimensions are large. This framework applies to any fixed stepsize and the finite sum setting. Using this new framework, we show that the dynamics of SGD on a least squares problem with random data become deterministic in the large sample and dimensional limit. Furthermore, the limiting dynamics are governed by a Volterra integral equation. This model predicts that SGD undergoes a phase transition at an explicitly given critical stepsize that ultimately affects its convergence rate, which we also verify experimentally.
Fourier-$L_\infty$ perturbations in the spatial
domain are concentrated around subtle details of the object
Bridging the Gap Between Adversarial Robustness and Optimization Bias, Fartash Faghri, Cristina Vasconcelos, David J. Fleet, Fabian Pedregosa, Nicolas Le Roux, under review, 2021. [ArXiv].
Abstract: We show that the choice of optimizer, neural network architecture, and regularizer significantly affect the adversarial robustness of linear neural networks, providing guarantees without the need for adversarial training. To this end, we revisit a known result linking maximally robust classifiers and minimum norm solutions, and combine it with recent results on the implicit bias of optimizers. First, we show that, under certain conditions, it is possible to achieve both perfect standard accuracy and a certain degree of robustness, simply by training an overparametrized model using the implicit bias of the optimization.
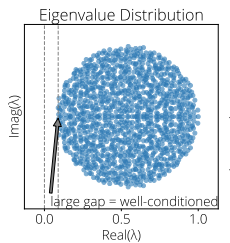
Eigenvalue distribution for the Jacobian of one of the games considered in this paper.
Average-case Acceleration for Bilinear Games and Normal Matrices, Carles Domingo-Enrich, Fabian Pedregosa, Damien Scieur, International Conference on Learning Representations (ICLR), 2021. [ArXiv], [Reviews], [Slides], [Talk].
Abstract: Average-case analysis computes the complexity of an algorithm averaged over all possible inputs. Compared to worst-case analysis, it is more representative of the typical behavior of an algorithm, but remains largely unexplored in optimization. One difficulty is that the analysis can depend on the probability distribution of the inputs to the model. However, we show that this is not the case for a class of large-scale problems trained with gradient descent including random least squares and one-hidden layer neural networks with random weights. In fact, the halting time exhibits a universality property: it is independent of the probability distribution. With this barrier for average-case analysis removed, we provide the first explicit average-case convergence rates showing a tighter complexity not captured by traditional worst-case analysis. Finally, numerical simulations suggest this universality property holds for a more general class of algorithms and problems.
The Geometry of Sign Gradient Descent, Lukas Balles, Fabian Pedregosa, Nicolas Le Roux, ArXiv, 2020. [ArXiv].
Abstract: Sign-based optimization methods have become popular in machine learning due to their favorable communication cost in distributed optimization and their surprisingly good performance in neural network training. Furthermore, they are closely connected to so-called adaptive gradient methods like Adam. Recent works on signSGD have used a non-standard "separable smoothness" assumption, whereas some older works study sign gradient descent as steepest descent with respect to the ℓ∞-norm. In this work, we unify these existing results by showing a close connection between separable smoothness and ℓ∞-smoothness and argue that the latter is the weaker and more natural assumption. We then proceed to study the smoothness constant with respect to the ℓ∞-norm and thereby isolate geometric properties of the objective function which affect the performance of sign-based methods. In short, we find sign-based methods to be preferable over gradient descent if (i) the Hessian is to some degree concentrated on its diagonal, and (ii) its maximal eigenvalue is much larger than the average eigenvalue. Both properties are common in deep networks.
Stochastic Frank-Wolfe for Constrained Finite-Sum Minimization, Geoffrey Négiar, Gideon Dresdner, Alicia Tsai, Laurent El Ghaoui, Francesco Locatello, Robert M. Freund, Fabian Pedregosa, Proceedings of the 37th International Conference on Machine Learning (ICML), 2020. [ArXiv], [Video], [Proceedings].
Abstract: We propose a novel Stochastic Frank-Wolfe (a.k.a. conditional gradient) algorithm for constrained smooth finite-sum minimization with a generalized linear prediction/structure. This class of problems includes empirical risk minimization with sparse, low-rank, or other structured constraints. The proposed method is simple to implement, does not require step-size tuning, and has a constant per-iteration cost that is independent of the dataset size. Furthermore, as a byproduct of the method we obtain a stochastic estimator of the Frank-Wolfe gap that can be used as a stopping criterion. Depending on the setting, the proposed method matches or improves on the best computational guarantees for Stochastic Frank-Wolfe algorithms. Benchmarks on several datasets highlight different regimes in which the proposed method exhibits a faster empirical convergence than related methods. Finally, we provide an implementation of all considered methods in an open-source package.
As it turns out, there's really only one optimal method in optimization: Polyak Momentum.
Universal Average-Case Optimality of Polyak Momentum, Damien Scieur, Fabian Pedregosa, Proceedings of the 37th International Conference on Machine Learning (ICML), 2020. [ArXiv], [Video], [BibTex].
Abstract: Polyak momentum (PM), also known as the heavy-ball method, is a widely used optimization method that enjoys an asymptotic optimal worst-case complexity on quadratic objectives. However, its remarkable empirical success is not fully explained by this optimality, as the worst-case analysis --contrary to the average-case-- is not representative of the expected complexity of an algorithm. In this work we establish a novel link between PM and the average-case analysis. Our main contribution is to prove that any optimal average-case method converges in the number of iterations to PM, under mild assumptions. This brings a new perspective on this classical method, showing that PM is asymptotically both worst-case and average-case optimal.
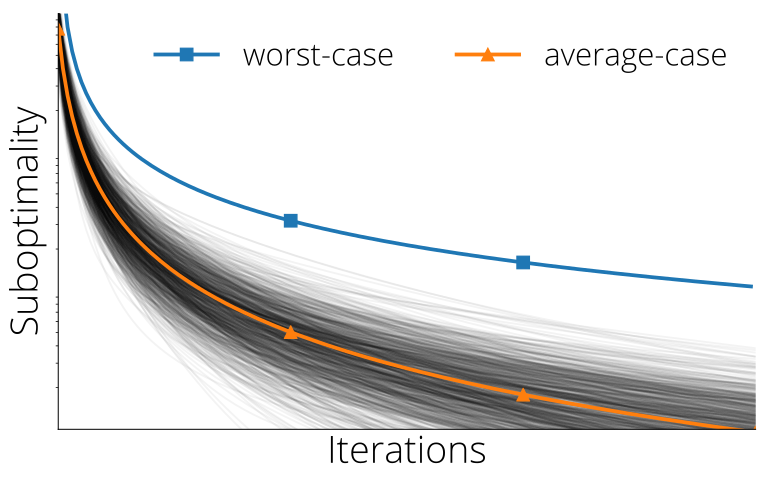
A worst-case analysis can lead to misleading results
where the worst-case running times is much worse than the observed running time. Above: convergence of individual random
square least squares in gray, while the average suboptimality (orange) is well below the worst-case (blue)
Average-case Acceleration Through Spectral Density Estimation, Fabian Pedregosa, Damien Scieur, Proceedings of the 37th International Conference on Machine Learning (ICML), 2020. [ArXiv], [Slides], [Video], [BibTex].
Abstract: We develop a framework for designing optimal quadratic optimization methods in terms of their average-case runtime. This yields a new class of methods that achieve acceleration through a model of the Hessian's expected spectral density. We develop explicit algorithms for the uniform, Marchenko-Pastur, and exponential distributions. These methods are momentum-based gradient algorithms whose hyper-parameters can be estimated without knowledge of the Hessian's smallest singular value, in contrast with classical accelerated methods like Nesterov acceleration and Polyak momentum. Empirical results on quadratic, logistic regression and neural networks show the proposed methods always match and in many cases significantly improve over classical accelerated methods.
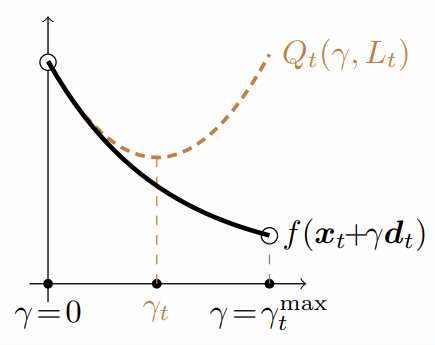
The sufficient decrease condition ensures that the quadratic approximation is an upper bound at its constrained minimum of the line-search objective.
Linearly Convergent Frank-Wolfe with Backtracking Line-Search, Fabian Pedregosa, Geoffrey Negiar, Armin Askari, Martin Jaggi. Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics (AISTATS), 2020. [ArXiv], [Slides], [Proceedings], [Video].
Abstract: Structured constraints in Machine Learning have recently brought the Frank-Wolfe (FW) family of algorithms back in the spotlight. While the classical FW algorithm has poor local convergence properties, the Away-steps and Pairwise FW variants have emerged as improved variants with faster convergence. However, these improved variants suffer from two practical limitations: they require at each iteration to solve a 1-dimensional minimization problem to set the step-size and also require the Frank-Wolfe linear subproblems to be solved exactly. In this paper, we propose variants of Away-steps and Pairwise FW that lift both restrictions simultaneously. The proposed methods set the step-size based on a sufficient decrease condition, and do not require prior knowledge of the objective. Furthermore, they inherit all the favorable convergence properties of the exact line-search version, including linear convergence for strongly convex functions over polytopes. Benchmarks on different machine learning problems illustrate large performance gains of the proposed variants.
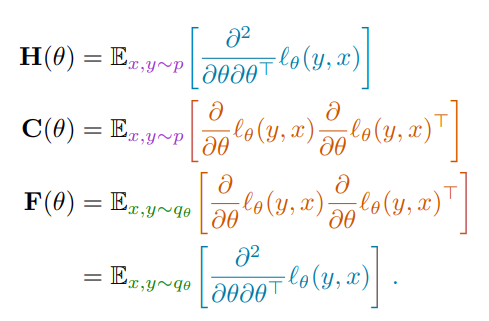Information matrices and generalization, Valentin Thomas, Fabian Pedregosa, Bart van Merriënboer, Pierre-Antoine Mangazol, Yoshua Bengio, Nicolas Le Roux. Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics (AISTATS) 2020.
Abstract: This work revisits the use of information criteria to characterize the generalization of deep learning models. In particular, we empirically demonstrate the effectiveness of the Takeuchi information criterion (TIC), an extension of the Akaike information criterion (AIC) for misspecified models, in estimating the generalization gap, shedding light on why quantities such as the number of parameters cannot quantify generalization. The TIC depends on both the Hessian of the loss H and the covariance of the gradients C. By exploring the similarities and differences between these two matrices as well as the Fisher information matrix F, we study the interplay between noise and curvature in deep models. We also address the question of whether C is a reasonable approximation to F, as is commonly assumed.
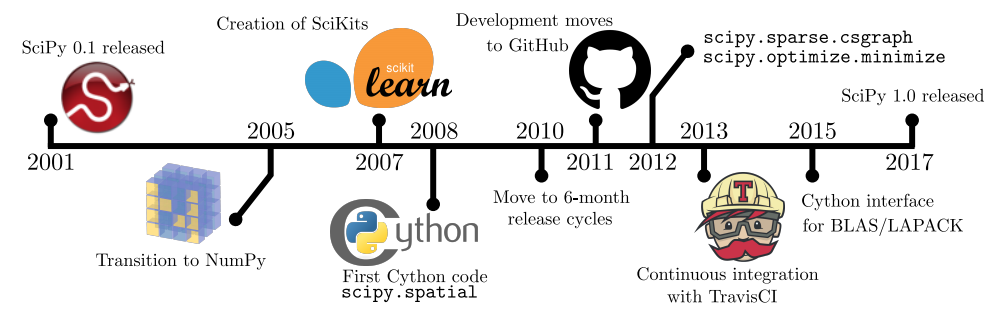
Major milestones from SciPy’s initial release in 2001 to the release of SciPy 1.0 in 2017.
SciPy 1.0--Fundamental Algorithms for Scientific Computing in Python, Pauli Virtanen, Ralf Gommers, Travis E. Oliphant, Matt Haberland, Tyler Reddy, David Cournapeau, Evgeni Burovski, Pearu Peterson, Warren Weckesser, Jonathan Bright, Stéfan J. van der Walt, Matthew Brett, Joshua Wilson, K. Jarrod Millman, Nikolay Mayorov, Andrew R. J. Nelson, Eric Jones, Robert Kern, Eric Larson, CJ Carey, İlhan Polat, Yu Feng, Eric W. Moore, Jake VanderPlas, Denis Laxalde, Josef Perktold, Robert Cimrman, Ian Henriksen, E.A. Quintero, Charles R Harris, Anne M. Archibald, Antônio H. Ribeiro, Fabian Pedregosa, Paul van Mulbregt, SciPy 1.0 Contributors [ArXiv].
Abstract: SciPy is an open source scientific computing library for the Python programming language. SciPy 1.0 was released in late 2017, about 16 years after the original version 0.1 release. SciPy has become a de facto standard for leveraging scientific algorithms in the Python programming language, with more than 600 unique code contributors, thousands of dependent packages, over 100,000 dependent repositories, and millions of downloads per year. This includes usage of SciPy in almost half of all machine learning projects on GitHub, and usage by high profile projects including LIGO gravitational wave analysis and creation of the first-ever image of a black hole (M87). The library includes functionality spanning clustering, Fourier transforms, integration, interpolation, file I/O, linear algebra, image processing, orthogonal distance regression, minimization algorithms, signal processing, sparse matrix handling, computational geometry, and statistics. In this work, we provide an overview of the capabilities and development practices of the SciPy library and highlight some recent technical developments.
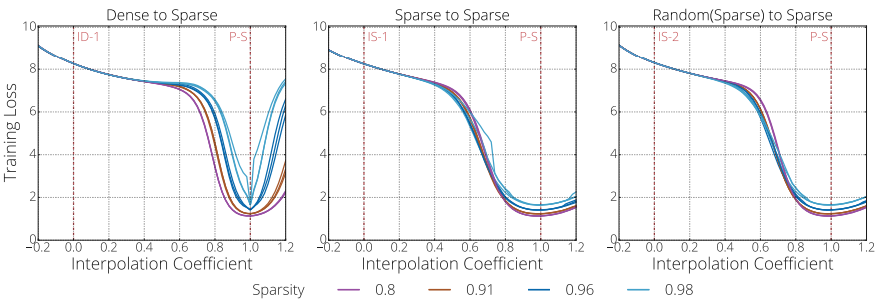
We find a monotonically decreasing path between different initializations and a set of "good" solutions found through pruning.
The Difficulty of Training Sparse Neural Networks, Utku Evci, Fabian Pedregosa, Aidan Gomez, Erich Elsen, 2019. [ArXiv]
Abstract: This work revisits the use of information criteria to characterize the generalization of deep learning models. In particular, we empirically demonstrate the effectiveness of the Takeuchi information criterion (TIC), an extension of the Akaike information criterion (AIC) for misspecified models, in estimating the generalization gap, shedding light on why quantities such as the number of parameters cannot quantify generalization. The TIC depends on both the Hessian of the loss H and the covariance of the gradients C. By exploring the similarities and differences between these two matrices as well as the Fisher information matrix F, we study the interplay between noise and curvature in deep models. We also address the question of whether C is a reasonable approximation to F, as is commonly assumed.
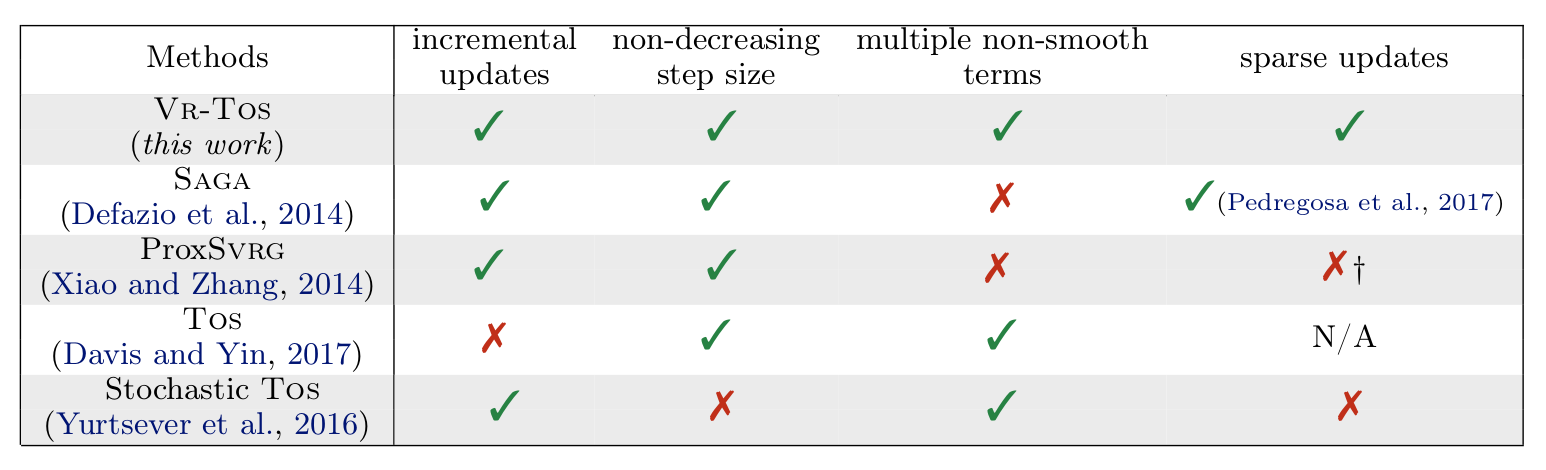The proposed method combines the advantages of variance-reduced methods (incremental updates, non-decreasing step sizes and sparse updates) with those of proximal splitting methods (support for a sum of non-smooth terms).
Proximal Splitting Meets Variance Reduction, Fabian Pedregosa, Kilian Fatras, Mattia Casotto, 2018. Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics. Proceedings version.
Abstract: Despite the rise to fame of incremental variance-reduced methods in recent years, their use in nonsmooth optimization is still limited to few simple cases. This is due to the fact that existing methods require to evaluate the proximity operator for the nonsmooth terms, which can be a costly operation for complex penalties. In this work we introduce two variance-reduced incremental methods based on SAGA and SVRG that can efficiently take into account complex penalties which can be expressed as a sum of proximal terms. This includes penalties such as total variation, group lasso with overlap and trend filtering, to name a few. Furthermore, we also develop sparse variants of the proposed algorithms which can take advantage of sparsity in the input data. Like other incremental methods, it only requires to evaluate the gradient of a single sample per iteration, and so is ideally suited for large scale applications. We provide a convergence rate analysis for the proposed methods and show that they converge with a fixed step-size, achieving in some cases the same asymptotic rate as their full gradient variants. Empirical benchmarks on 3 different datasets illustrate the practical advantages of the proposed methods.
In the proposed method, the candidate step size must verify a sufficient decrease condition, which can be interpreted as a quadratic upper bound on the objective function.
Adaptive Three Operator Splitting, Fabian Pedregosa, Gauthier Gidel, Proceedings of the 35th International Conference on Machine Learning, 2018. ICML, [ArXiv], [Slides], [Poster], [Video] (starts at minute 52).
Abstract: We propose and analyze a novel adaptive step size variant of the Davis-Yin three operator splitting, a method that can solve optimization problems composed of a sum of a smooth term for which we have access to its gradient and an arbitrary number of potentially non-smooth terms for which we have access to their proximal operator. The proposed method leverages local information of the objective function, allowing for larger step sizes while preserving the convergence properties of the original method. It only requires two extra function evaluations per iteration and does not depend on any step size hyperparameter besides an initial estimate. We provide a convergence rate analysis of this method, showing sublinear convergence rate for general convex functions and linear convergence under stronger assumptions, matching the best known rates of its non adaptive variant. Finally, an empirical comparison with related methods on 6 different problems illustrates the computational advantage of the adaptive step size strategy.
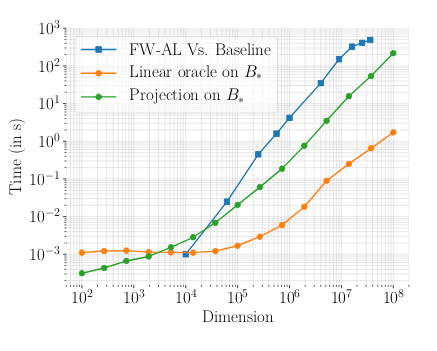
We propose a step-size for the Frank-Wolfe and Matching Pursuit algorithms that only depends on local information of the objective. This allows to take larger step-sizes and converge faster.
Frank-Wolfe Splitting via Augmented Lagrangian Method, Gauthier Gidel, Fabian Pedregosa, Simon Lacoste-Julien, Proceedings of the Twenty-First International Conference on Artficial Intelligence and Statistics, 2018. [PDF], [PDF supplementary], [Poster], [Slides]
Abstract: Minimizing a function over an intersection of convex sets is an important task in optimization that is often much more challenging than minimizing it over each individual constraint set. While traditional methods such as Frank-Wolfe (FW) or proximal gradient descent assume access to a linear or quadratic oracle on the intersection, splitting techniques take advantage of the structure of each sets, and only require access to the oracle on the individual constraints. In this work, we develop and analyze the Frank-Wolfe Augmented Lagrangian (FW-AL) algorithm, a method for minimizing a smooth function over convex compact sets related by a “linear consistency” constraint that only requires access to a linear minimization oracle over the individual constraints. It is based on the Augmented Lagrangian Method (ALM), also known as Method of Multipliers, but unlike most existing splitting methods, it only requires access to linear (instead of quadratic) minimization oracles. We use recent advances in the analysis of Frank-Wolfe and the alternating direction method of multipliers algorithms to prove a sublinear convergence rate for FW-AL over general convex compact sets and a linear convergence rate for polytopes.
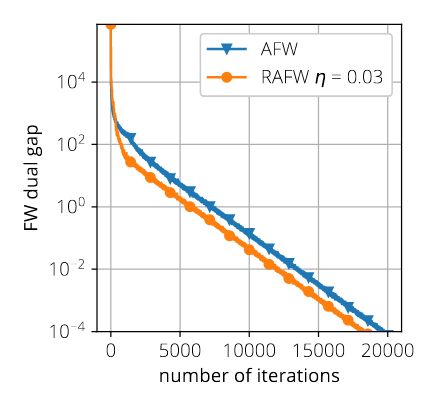
The Randomized Away-steps FW variant that we propose (RAFW) is competitive with Away-steps FW (AFW), albeit with a much smaller per iteration cost.
Frank-Wolfe with Subsampling Oracle, Thomas Kerdreux, Fabian Pedregosa, Alexandre d'Aspremont, Proceedings of the 35th International Conference on Machine Learning, 2018. ICML, [ArXiv]
Abstract: We analyze two novel randomized variants of the Frank-Wolfe (FW) or conditional gradient algorithm. While classical FW algorithms require solving a linear minimization problem over the domain at each iteration, the proposed method only requires to solve a linear minimization problem over a small subset of the original domain. The first algorithm that we propose is a randomized variant of the original FW algorithm and achieves a (1/t) sublinear convergence rate as in the deterministic counterpart. The second algorithm is a randomized variant of the Away-step FW algorithm, and again as its deterministic counterpart, reaches linear (i.e., exponential) convergence rate making it the first provably convergent randomized variant of Away-step FW. In both cases, while subsampling reduces the convergence rate by a constant factor, the linear minimization step can be a fraction of the cost of that of the deterministic versions, especially when the data is streamed. We illustrate computational gains of the algorithms on regression problems, involving both L1 and latent group lasso penalties .
In this paper we highlight an issue present in large part of the literature of asynchronous stochastic optimization: under the traditional labeling scheme (i.e., how the iterates are named), gradient estimates might be biased. We propose a solution to this issue via a different labeling scheme.
Improved asynchronous parallel optimization analysis for stochastic incremental methods, Rémi Leblond, Fabian Pedregosa, Simon Lacoste-Julien, 2018. Journal of Machine Learning Research
Abstract: As datasets continue to increase in size and multi-core computer architectures are developed, asynchronous parallel optimization algorithms become more and more essential to the field of Machine Learning. Through a novel perspective, we revisit and clarify a subtle but important technical issue present in a large fraction of the recent convergence rate proofs for asynchronous parallel optimization algorithms, and propose a simplification of the recently introduced "perturbed iterate" framework that resolves it. We demonstrate the usefulness of our new framework by analyzing three distinct asynchronous parallel incremental optimization algorithms: Hogwild (asynchronous SGD), KROMAGNON (asynchronous SVRG) and ASAGA, a novel asynchronous parallel version of the incremental gradient algorithm SAGA that enjoys fast linear convergence rates.
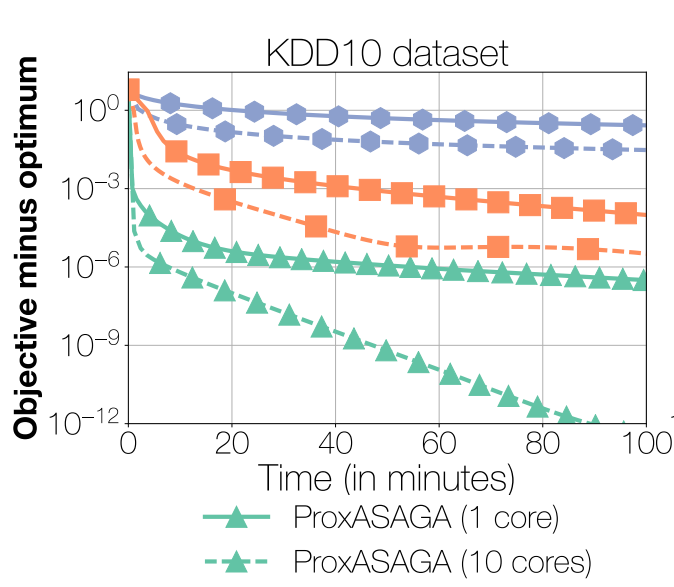
ProxASAGA achieves significant speedups over its sequential
version while being orders of magnitude faster than competing methods.
Breaking the Nonsmooth Barrier: A Scalable
Parallel Method for Composite Optimization, Fabian Pedregosa, Rémi Leblond, Simon Lacoste-Julien. Advances in Neural Information Processing Systems 30 (NIPS), 2017. Spotlight presentation (top 3% of submitted papers). NIPS, [ArXiv], Github, [BibTex], [Video], Poster.
Abstract: Due to their simplicity and excellent performance, parallel asynchronous variants of stochastic gradient descent have become popular methods to solve a wide range of large-scale optimization problems on multi-core architectures. Yet, despite their practical success, support for nonsmooth objectives is still lacking, making them unsuitable for many problems of interest in machine learning, such as the Lasso, group Lasso or empirical risk minimization with convex constraints. In this work, we propose and analyze ProxASAGA, a fully asynchronous sparse method inspired by SAGA, a variance reduced incremental gradient algorithm. The proposed method is easy to implement and significantly outperforms the state of the art on several nonsmooth, large-scale problems. We prove that our method achieves a theoretical linear speedup with respect to the sequential version under assumptions on the sparsity of gradients and block-separability of the proximal term. Empirical benchmarks on a multi-core architecture illustrate practical speedups of up to 12x on a 20-core machine.
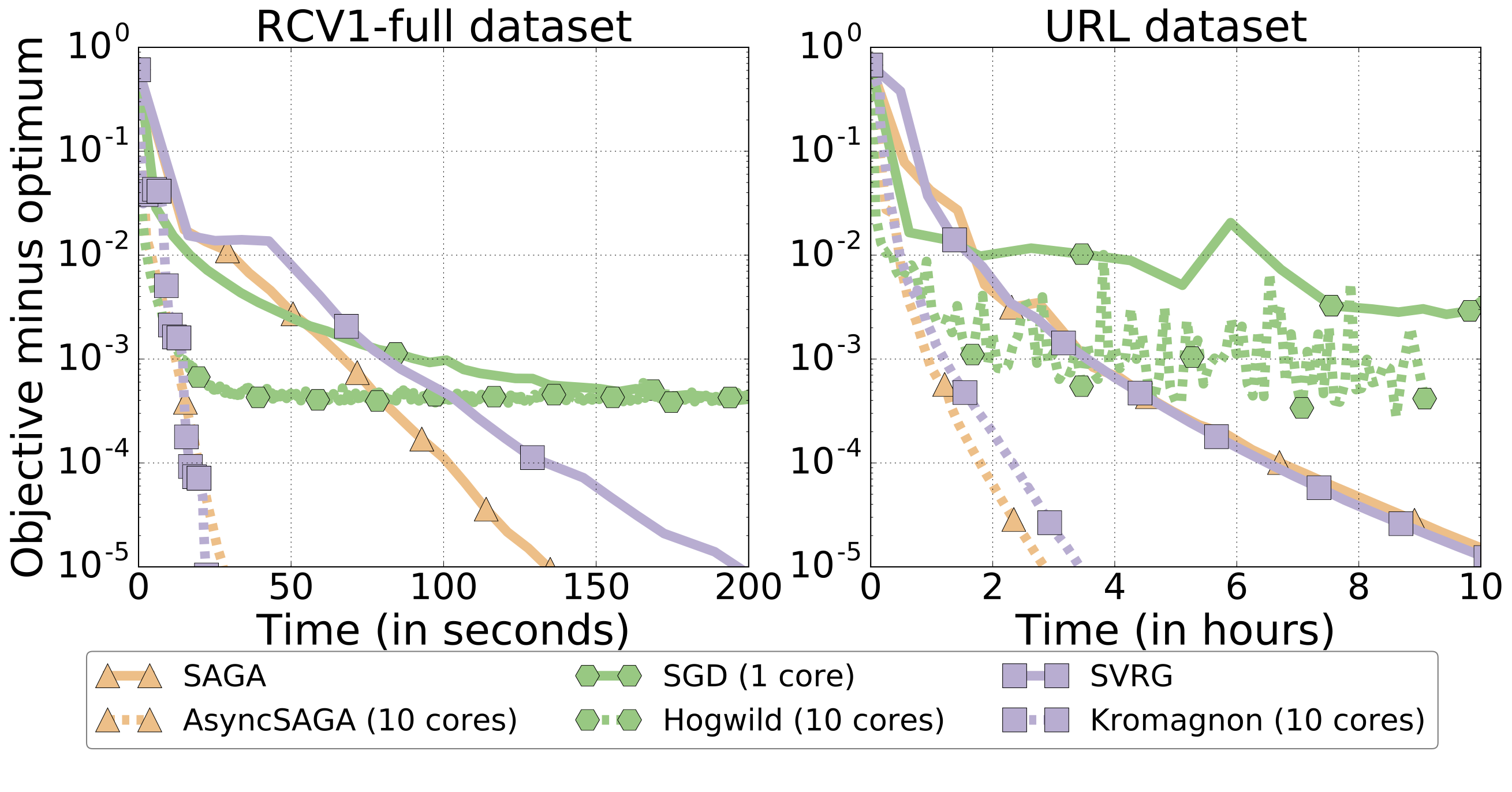
ASAGA is simple asynchronous algorithm that achieves state of the art performance and significant speedups on parallel processors. Above, a 5x speedup on 10 processors over its sequential version on two different datasets.
ASAGA: Asynchronous Parallel SAGA, Rémi Leblond, Fabian Pedregosa, Simon Lacoste-Julien. Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (AISTATS), 2017.
AISTATS [ArXiv], [Webpage], Github, [Blog post].
Abstract: We describe ASAGA, an asynchronous parallel version of the incremental gradient algorithm SAGA that enjoys fast linear convergence rates. Through a novel perspective, we revisit and clarify a subtle but important technical issue present in a large fraction of the recent convergence rate proofs for asynchronous parallel optimization algorithms, and propose a simplification of the recently introduced “perturbed iterate” framework that resolves it. We thereby prove that ASAGA can obtain a theoretical linear speedup on multi-core systems even without sparsity assumptions. We present results of an implementation on a 40-core architecture illustrating the practical speedup as well as the hardware overhead.
We characterize a the Fisher consistency of a rich family of loss functions commonly used in ordinal regression. Surprisingly, we discover that many such functions are consistent with respect to the 0-1 loss and not the absolute error.
On the Consistency of Ordinal Regression Methods, Fabian Pedregosa, Francis Bach, and Alexandre Gramfort, Journal of Machine Learning Research, 2017. JMLR, ArXiv, Blog post.
Abstract: Many of the ordinal regression models that have been proposed in the literature can be seen as methods that minimize a convex surrogate of the zero-one, absolute, or squared loss functions. A key property that allows to study the statistical implications of such approximations is that of Fisher consistency. Fisher consistency is a desirable property for surrogate loss functions and implies that in the population setting, i.e., if the probability distribution that generates the data were available, then optimization of the surrogate would yield the best possible model. In this paper we will characterize the Fisher consistency of a rich family of surrogate loss functions used in the context of ordinal regression, including support vector ordinal regression, ORBoosting and least absolute deviation.
This paper describes SymPy, a Python library for symbolic computations. Among other things, it can compute the symbolic expression for derivatives, integrals or compute the exact solution of some polynomial equations (think of $\sqrt{2}$ vs $1.4142...$). Check out its website and comprehensive documentation for more information.
SymPy: Symbolic computing in Python, Aaron Meurer, Christopher P. Smith, Mateusz Paprocki, Ondřej Čertík, Sergey B. Kirpichev, Matthew Rocklin, AmiT Kumar, Sergiu Ivanov, Jason K. Moore, Sartaj Singh, Thilina Rathnayake, Sean Vig, Brian E. Granger, Richard P. Muller, Francesco Bonazzi, Harsh Gupta, Shivam Vats, Fredrik Johansson, Fabian Pedregosa, Matthew J. Curry, Andy R. Terrel, Štěpán Roučka, Ashutosh Saboo, Isuru Fernando, Sumith Kulal, Robert Cimrman, Anthony Scopatz. PeerJ Computer Science, 2017. PeerJ.
Abstract: SymPy is an open source computer algebra system written in pure Python. It is built with a focus on extensibility and ease of use, through both interactive and programmatic applications. These characteristics have led SymPy to become a popular symbolic library for the scientific Python ecosystem. This paper presents the architecture of SymPy, a description of its features, and a discussion of select submodules. The supplementary material provide additional examples and further outline details of the architecture and features of SymPy.
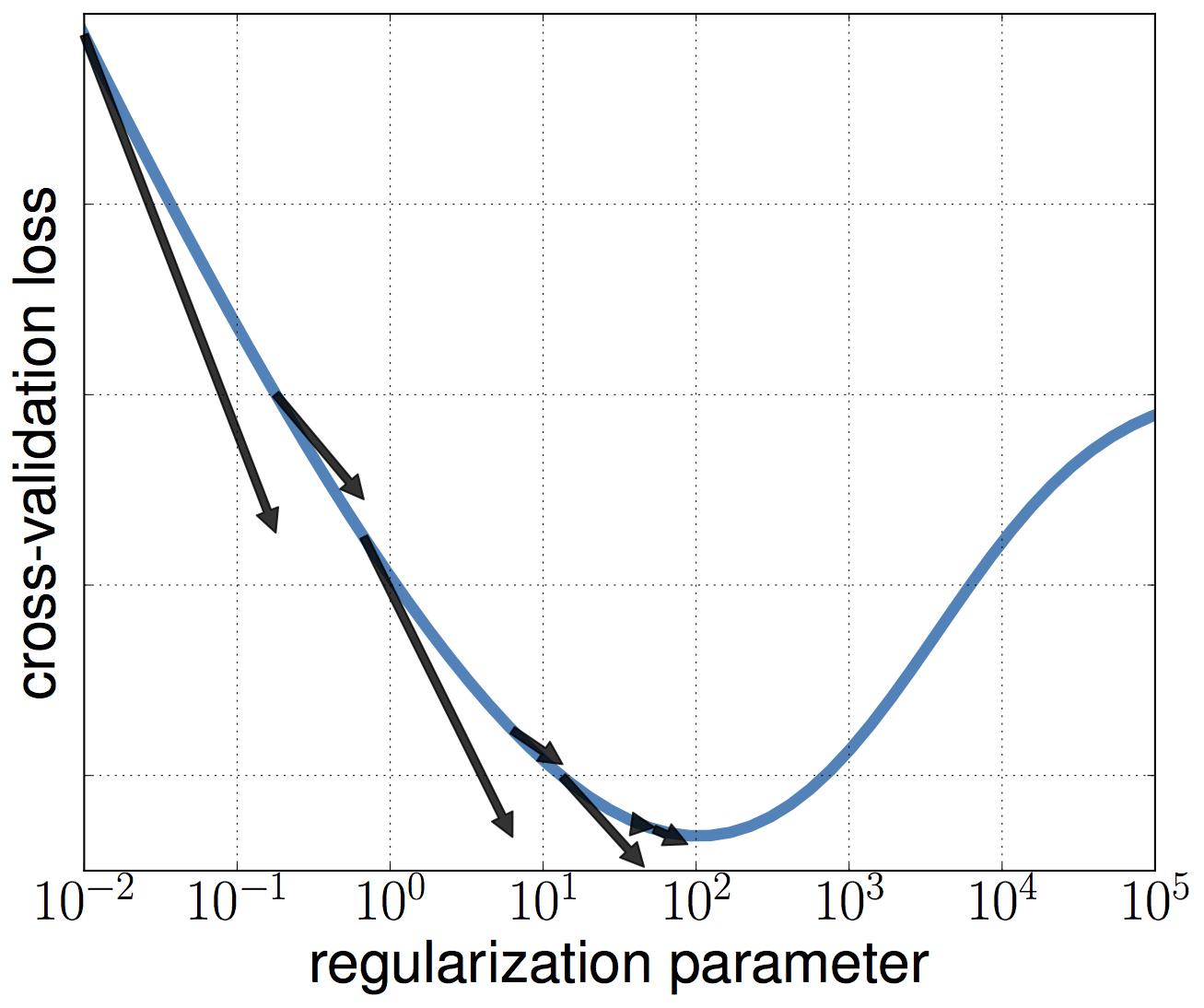
An approximate gradient can be used to optimize a cross-validation loss with respect to hyperparameters. A decreasing bound between the true gradient and the approximate ensures the method converges towards a stationary point.
Hyperparameter optimization with approximate gradient, Fabian Pedregosa,
Proceedings of The 33rd International Conference on Machine Learning, 2016. [ICML], [ArXiv], [Slides], [Code], [Blog post].
Abstract: Most models in machine learning contain at least one hyperparameter to control for model complexity. Choosing an appropriate set of hyperparameters is both crucial in terms of model accuracy and computationally challenging. In this work we propose an algorithm for the optimization of continuous hyperparameters using inexact gradient information. An advantage of this method is that hyperparameters can be updated before model parameters have fully converged. We also give sufficient conditions for the global convergence of this method, based on regularity conditions of the involved functions and summability of errors. Finally, we validate the empirical performance of this method on the estimation of regularization constants of L2-regularized logistic regression and kernel Ridge regression. Empirical benchmarks indicate that our approach is highly competitive with respect to state of the art methods.
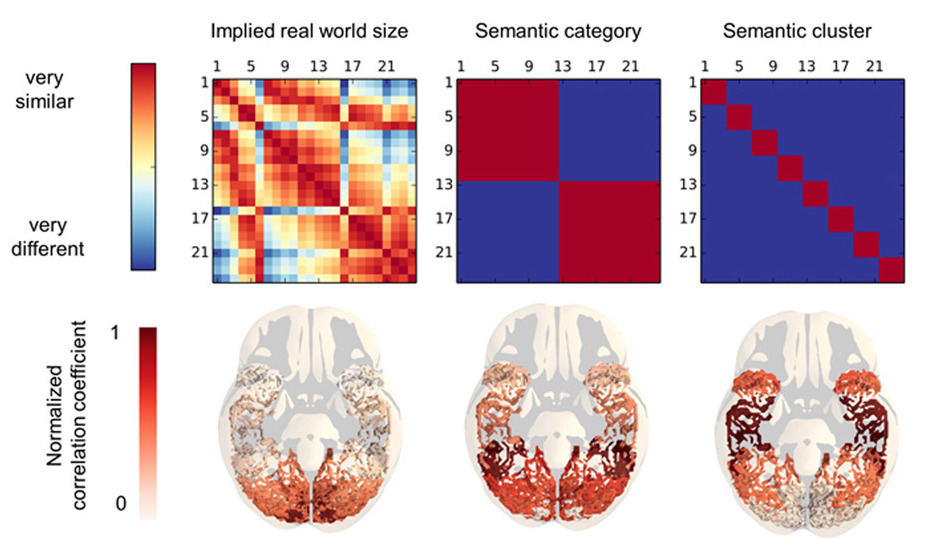
How is the meaning of words instantiated in the brain?. Our results indicate that different aspects of word meaning are encoded in a distributed way
across different brain areas. Word meaning in the ventral visual path: a perceptial to conceptual gradient of semantic coding. Valentina Borghesani, Fabian Pedregosa, Marco Buiatti, Alexis Amadon, Evelyn Eger, and Manuela Piazza. NeuroImage, 2016.
PDF, NeuroImage, ResearchGate.
Abstract: The meaning of words referring to concrete items is thought of as a multidimensional representation that includes both perceptual (e.g., average size, prototypical color) and conceptual (e.g., taxonomic class) dimensions. Are these different dimensions coded in different brain regions? In healthy human subjects, we tested the presence of a mapping between the implied real object size (a perceptual dimension) and the taxonomic categories at different levels of specificity (conceptual dimensions) of a series of words, and the patterns of brain activity recorded with functional magnetic resonance imaging in six areas along the ventral occipito-temporal cortical path. Combining multivariate pattern classification and representational similarity analysis, we found that the real object size implied by a word appears to be primarily encoded in early visual regions, while the taxonomic category and sub-categorical cluster in more anterior temporal regions. This anteroposterior gradient of information content indicates that different areas along the ventral stream encode complementary dimensions of the semantic space.
Short technical report that simplifies some of the convergence proofs for the Davis-Yin three operator splitting method. On the convergence rate of the three operator splitting scheme, Fabian Pedregosa. ArXiv:1610.07830
Abstract: The three operator splitting scheme was recently proposed by [Davis and Yin, 2015] as a method to optimize composite objective functions with one convex smooth term and two convex (possibly non-smooth) terms for which we have access to their proximity operator. In this short note we provide an alternative proof for the sublinear rate of convergence of this method.
One of the key aspects investigated in this thesis is the estimation of brain maps from a blood-oxygen-level dependent (BOLD) signal. One of the difficulties in this process stems from the fact that the BOLD signal does not
increase instantaneously after the stimuli onset nor does it return to baseline
immediately after the stimulus onset. Instead, it peaks
approximately 5 seconds after stimulation, and is followed by an undershoot
that lasts as long as 30 seconds.
PhD thesis: Feature extraction and supervised learning on fMRI: from practice to theory, defended February 2015 [PDF] [slides]
Advisors: Alexandre Gramfort (Telecom Paristech, Paris, France) and Francis Bach (INRIA / ENS, Paris, France).
Reviewers: Dimitri Van de Ville (Univ. Geneva / EPFL, Geneva, CH) and Alain Rakotomamonjy (University of Rouen, Rouen, France).
Jury: Marcel Van Gerven (Donders Instute, Nijmegen, NL), Ludovic Denoyer ( UPMC, Paris, France), Bertrand Thirion (INRIA / CEA, Saclay, France)
Abstract: Until the advent of non-invasive neuroimaging modalities the knowledge of the human brain came from the study of its lesions, post-mortem analyses and invasive experimentations. Nowadays, modern imaging techniques such as fMRI are revealing several aspects of the human brain with progressively high spatio-temporal resolution. However, in order to answer increasingly complex neuroscientific questions the technical improvements in acquisition must be matched with novel data analysis methods. In this thesis we examine different applications of machine learning to the processing of fMRI data. We propose novel extensions and investigate the theoretical properties of different models...
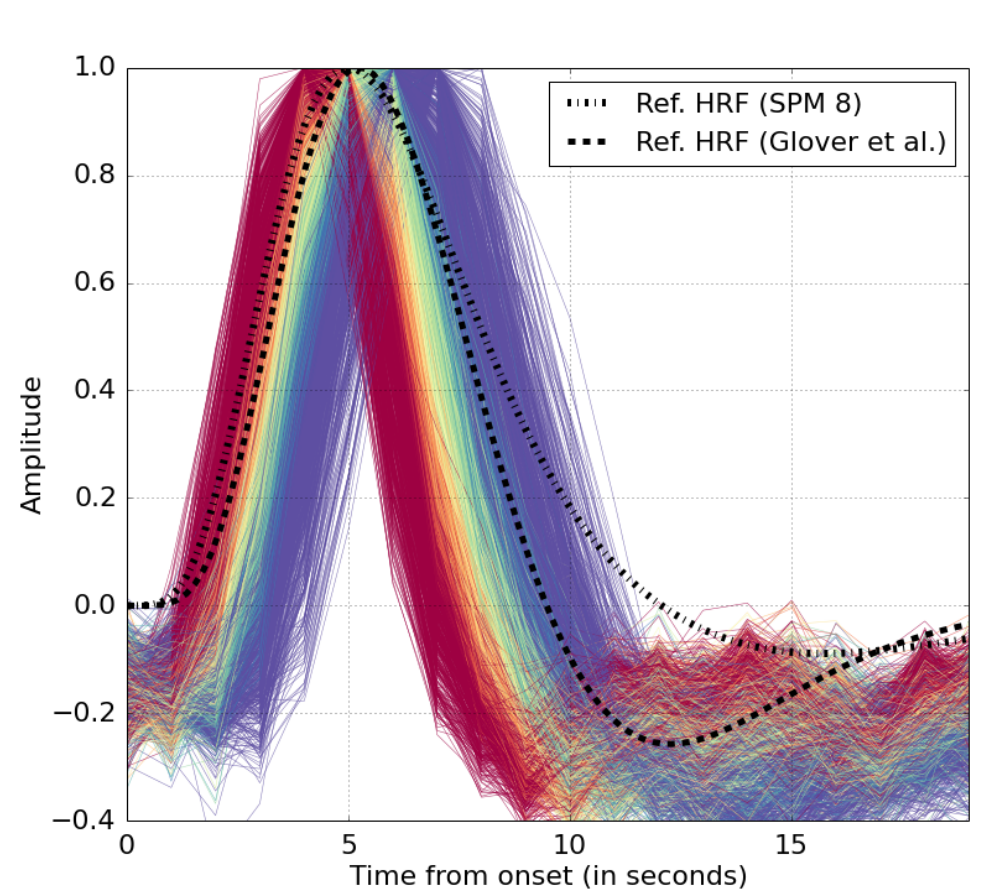We describe a method to estimate the hemodynamical response function (HRF) from an fMRI signal. Our method allows to estimate a different HRF per voxel. The difference in the estimated HRFs suggests a substantial
variability at the voxel level within a single subject and a single task.
Data-driven HRF estimation for encoding and decoding models, Fabian Pedregosa, Michael Eickenberg, Philippe Ciuciu, Bertrand Thirion, and Alexandre Gramfort. Neuroimage, 2015. ArXiv, NeuroImage
Abstract: Despite the common usage of a canonical, data-independent, hemodynamic response function (HRF), it is known that the shape of the HRF varies across brain regions and subjects. This suggests that a data-driven estimation of this function could lead to more statistical power when modeling BOLD fMRI data. However, unconstrained estimation of the HRF can yield highly unstable results when the number of free parameters is large. We develop a method for the joint estimation of activation and HRF by means of a rank constraint, forcing the estimated HRF to be equal across events or experimental conditions, yet permitting it to differ across voxels. Model estimation leads to an optimization problem that we propose to solve with an efficient quasi-Newton method, exploiting fast gradient computations. This model, called GLM with Rank-1 constraint (R1-GLM), can be extended to the setting of GLM with separate designs which has been shown to improve decoding accuracy in brain activity decoding experiments. We compare 10 different HRF modeling methods in terms of encoding and decoding scores on two different datasets. Our results show that the R1-GLM model outperforms competing methods in both encoding and decoding settings, positioning it as an attractive method both from the points of view of accuracy and computational efficiency.
Correlations of correlations are not reliable statistics: implications for multivariate pattern analysis. Bertrand Thirion, Fabian Pedregosa, Michael Eickenberg, Gael Varoquaux, ICML Workshop on Statistics, Machine Learning and Neuroscience (Stamlins 2015) PDF
A perceptual-to-conceptual gradient of word coding along the ventral path Valentina Borghesani, Fabian Pedregosa, Evelyn Eger, Marco Buiatti, Manuela Piazza. 4th International Workshop in Pattern Recognition and Neuroimaging, 2014. [PDF]
Machine learning for neuroimaging with scikit-learn, Alexandre Abraham, Fabian Pedregosa, Michael Eickenberg, Philippe Gervais, Andreas Mueller, Jean Kossaifi, Alexandre Gramfort, Bertrand Thirion, Gaël Varoquaux. Frontiers in Neuroinformatics, 2014. [link]
API design for machine learning software: experiences from the scikit-learn project, Lars Buitinck, Gilles Louppe, Mathieu Blondel, Fabian Pedregosa, Andreas Mueller, Olivier Grisel, Vlad Niculae, Peter Prettenhofer, Alexandre Gramfort, Jaques Grobler, Robert Layton, Jake Vanderplas, Arnaud Joly, Brian Holt, Gaël Varoquaux. European Conference on Machine Learning and Principles and Practices of Knowledge Discovery in Databases, 2013. [ArXiv]
HRF estimation improves sensitivity of fMRI encoding and decoding models, Fabian Pedregosa, Michael Eickenberg, Bertrand Thirion, Alexandre Gramfort. International Workshop on Pattern Recognition in Neuroimaging (PRNI), 2013. [ArXiv]
Second order scattering descriptors predict fMRI activity due to visual textures, Michael Eickenberg, Mehdi Senoussi, Fabian Pedregosa, Alexandre Gramfort, Bertrand Thirion. International Workshop on Pattern Recognition in Neuroimaging (PRNI), 2013. [ArXiv]
Learning to rank from medical imaging data, Fabian Pedregosa et al. in Proc. 3rd Int. Work. Mach. Learn. Med. Imaging (2012). [ArXiv] [ArXiv]
Scikit-learn : Machine Learning in Python, Fabian Pedregosa, Gaël Varoquaux, Alexandre Gramfort, Vincent Michel, Bertrand Thirion, Olivier Grisel, Mathieu Blondel, Peter Prettenhofer, Ron Weiss, Vincent Dubourg, Jake Vanderplas, Alexandre Passos, David Cournapeau, Matthieu Brucher, Matthieu Perrot, Édouard Duchesnay, Journal of Machine Learning Research, 2011. JMLR, PDF.
Abstract: Scikit-learn is a Python module integrating a wide range of state-of-the-art machine learning algorithms for medium-scale supervised and unsupervised problems. This package focuses on bringing machine learning to non-specialists using a general-purpose high-level language. Emphasis is put on ease of use, performance, documentation, and API consistency. It has minimal dependencies and is distributed under the simplified BSD license, encouraging its use in both academic and commercial settings. Source code, binaries, and documentation can be downloaded from http://scikit-learn.org.
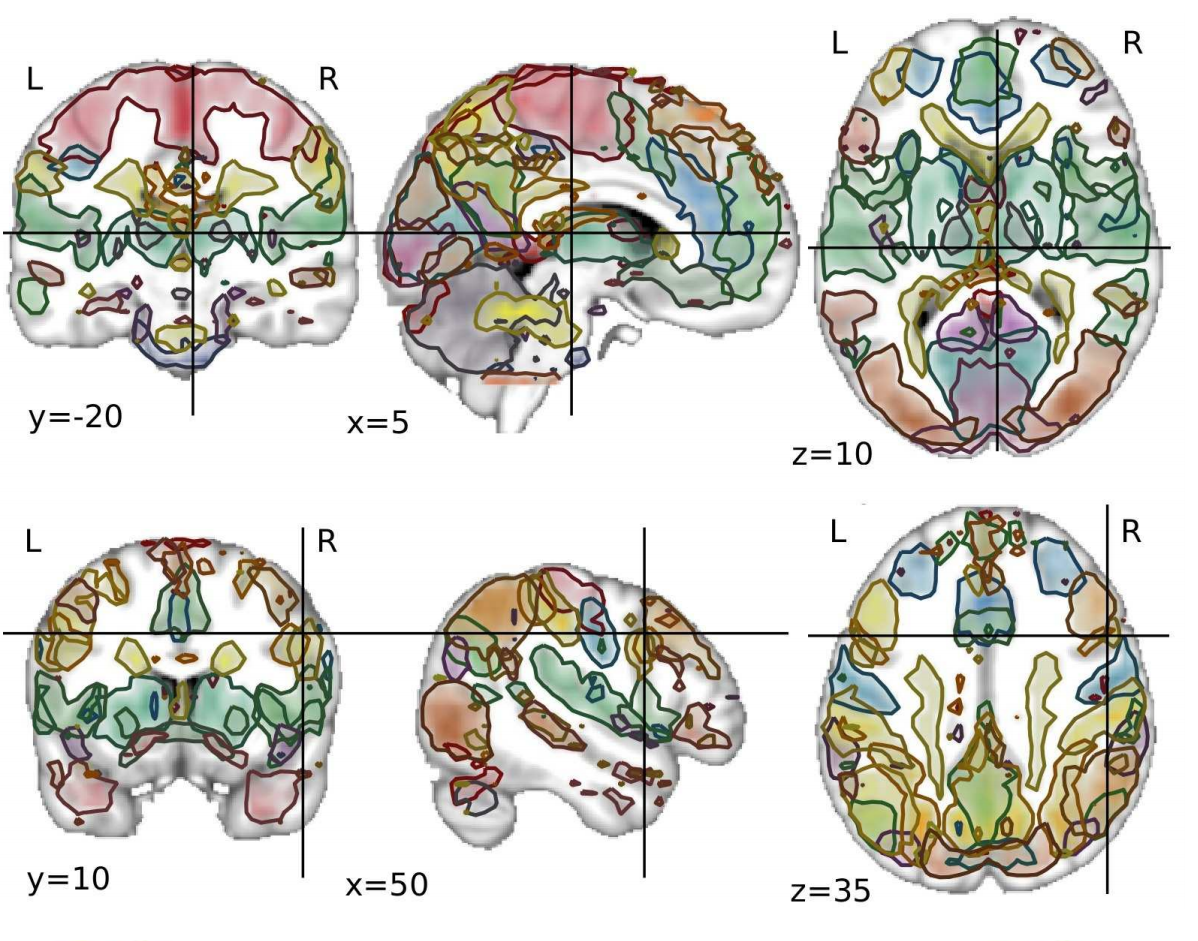Multi-subject dictionary learning to segment an atlas of brain spontaneous activity, Gaël Varoquaux, Alexandre Gramfort, Fabian Pedregosa, Vincent Michel, Bertrand Thirion. [PDF]
Abstract: Fluctuations in brain on-going activity can be used to reveal its intrinsic functional organization. To mine this information, we give a new hierarchical probabilistic model for brain activity patterns that does not require an experimental design to be specified. We estimate this model in the dictionary learning framework, learning simultaneously latent spatial maps and the corresponding brain activity time-series. Unlike previous dictionary learning frameworks, we introduce an explicit difference between subject-level spatial maps and their corresponding population-level maps, forming an atlas. We give a novel algorithm using convex optimization techniques to solve efficiently this problem with non-smooth penalties well-suited to image denoising. We show on simulated data that it can recover population-level maps as well as subject specificities. On resting-state fMRI data, we extract the first atlas of spontaneous brain activity and show how it defines a subject-specific functional parcellation of the brain in localized regions.