A fully asynchronous variant of the SAGA algorithm
My friend Rémi Leblond has recently uploaded to ArXiv our preprint on an asynchronous version of the SAGA optimization algorithm.
The main contribution is to develop a parallel (fully asynchronous, no locks) variant of the SAGA algorighm. This is a stochastic variance-reduced method for general optimization, specially adapted for problems that arise frequently in machine learning such as (regularized) least squares and logistic regression. Besides the specification of the algorithm, we also provide a convergence proof and convergence rates. Furthermore, we fix some subtle technical issues present in previous literature (proving things in the asynchronous setting is hard!).
The core of the asynchronous algorithm is similar to Hogwild!, a popular asynchronous variant of stochastc gradient descent (SGD). The main difference is that instead of using SGD as a building block, we use SAGA. This has many advantages (and poses some challenges): faster (exponential!) rates of convergence and convergence to arbitrary precision with a fixed step size (hence clear stopping criterion), to name a few.
The speedups obtained versus the sequential version are quite impressive. For example, we have observed to commonly obtain 5x-7x speedups using 10 cores:
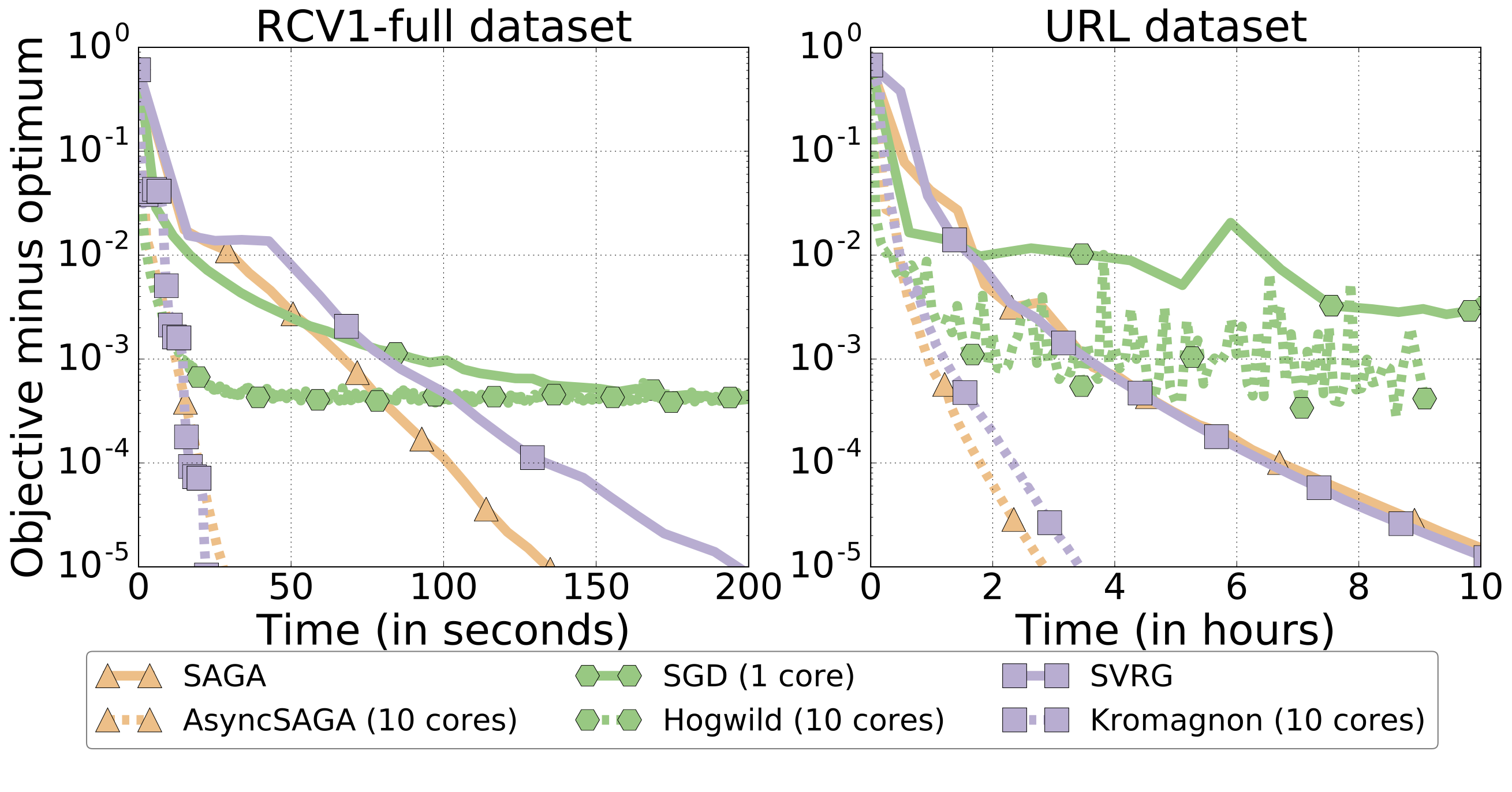
Update April 2017: this work has been presented at AISTATS 2017.
Had a great time presenting our work at #AISTATS2017, can't wait for the next edition! pic.twitter.com/W58K5IVRio
— Fabian Pedregosa (@fpedregosa) April 24, 2017
Update Dec 2017: a follow-up of this work generalizes the algorithm to the more general class of composite objective functions. See our paper "Breaking the Nonsmooth Barrier: A Scalable Parallel Method for Composite Optimization"