Isotonic Regression
My latest contribution for scikit-learn is an implementation of the isotonic regression model that I coded with Nelle Varoquaux and Alexandre Gramfort. This model finds the best least squares fit to a set of points, given the constraint that the fit must be a non-decreasing function. The example on the scikit-learn website gives an intuition on this model.
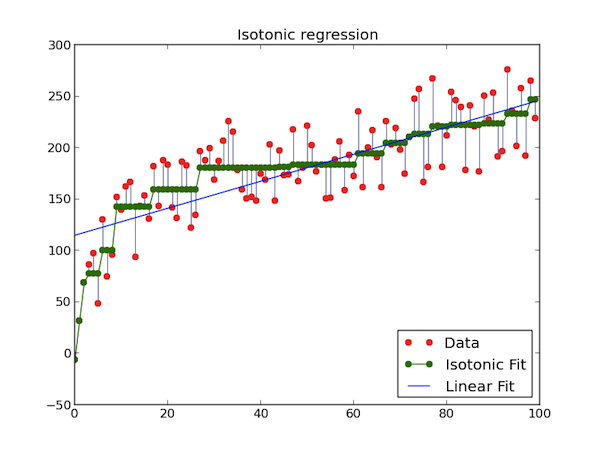
The original points are in red, and the estimated ones are in green. As you can see, there is one estimation (green point) for each data sample (red point). Calling $y \in \mathbb{R}^n$ the input data, the model can be written concisely as an optimization problem over $x$
$$ \text{argmin}_x |y - x |^2 \\ \text{subject to } x_0 \leq x_1 \leq \cdots \leq x_n $$
The algorithm implemented in scikit-learn 3 is the pool adjacent violators algorithm 1, which is an efficient linear time $\mathcal{O}(n)$ algorithm. The algorithm sweeps through the data looking for violations of the monotonicity constraint. When it finds one, it adjusts the estimate to the best possible fit with constraints. Sometimes it also needs to modify previous points to make sure the new estimate does not violate the constraints. The following picture shows how it proceeds at each iteration
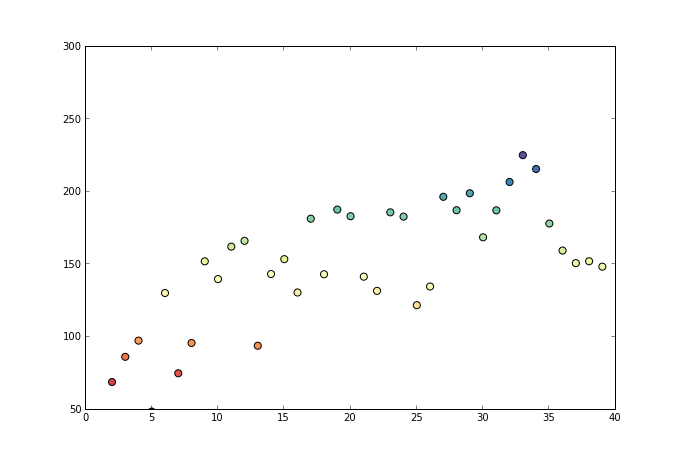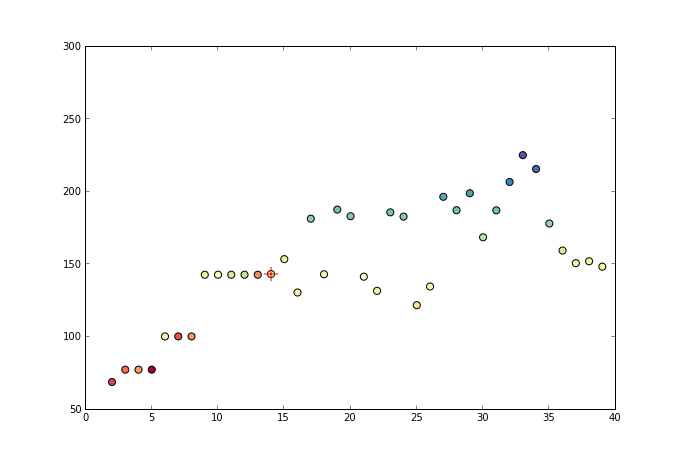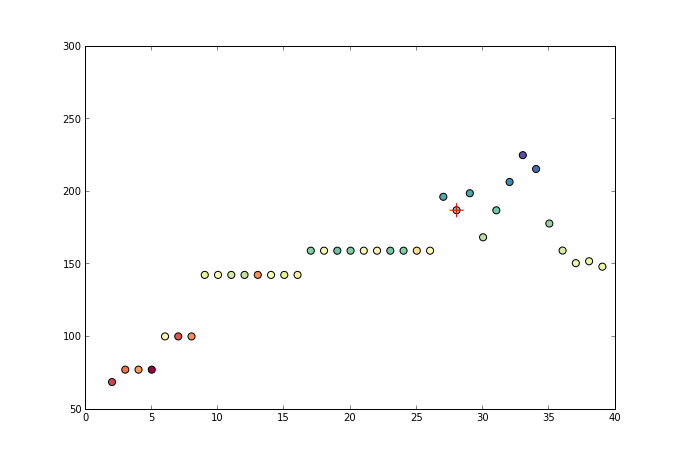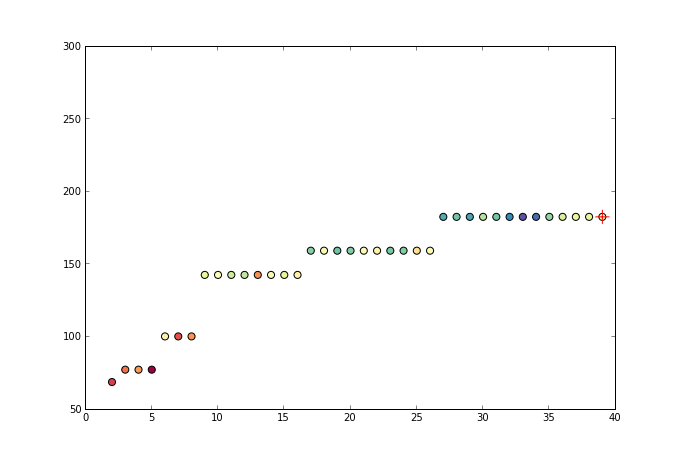
-
"Active set algorithms for isotonic regression; A unifying framework", Michael J. Best, Nilotpal Chakravarti ↩
-
Python notebook to generate the figures: ipynb and web version ↩
-
The algorithm is used through the sklearn.isotonic.IsotonicRegression object (doc) or the function sklearn.isotonic.isotonic_regression (doc) ↩