SAGA algorithm in the lightning library
Recently I've implemented, together with Arnaud Rachez, the SAGA[1] algorithm in the lightning machine learning library (which by the way, has been recently moved to the new scikit-learn-contrib project). The lightning library uses the same API as scikit-learn but is particularly adapted to online learning. As for the SAGA algorithm, its performance is similar to other variance-reduced stochastic algorithms such as SAG[3] or SVRG[2] but it has the advantage with respect to SAG[3] that it allows non-smooth penalty terms (such as $\ell_1$ regularization). It is implemented in lightning as SAGAClassifier and SAGARegressor.
We have taken care to make this implementation as efficient as possible. As for most stochastic gradient algorithms, a naive implementation takes 3 lines of code and is straightforward to implement. However, there are many tricks that are time-consuming and error-prone to implement but make a huge difference in efficiency.
A small example, more as a sanity check than to claim anything. The following plot shows the suboptimality as a function of time for three similar methods: SAG, SAGA and SVRG. The dataset used in the RCV1 dataset (test set, obtained from the libsvm webpage), consisting of 677.399 samples and 47.236 features. Interestingly, all methods can solve this rather large-scale problem within a few seconds. Within them, SAG and SAGA have a very similar performance and SVRG seems to be reasonably faster.
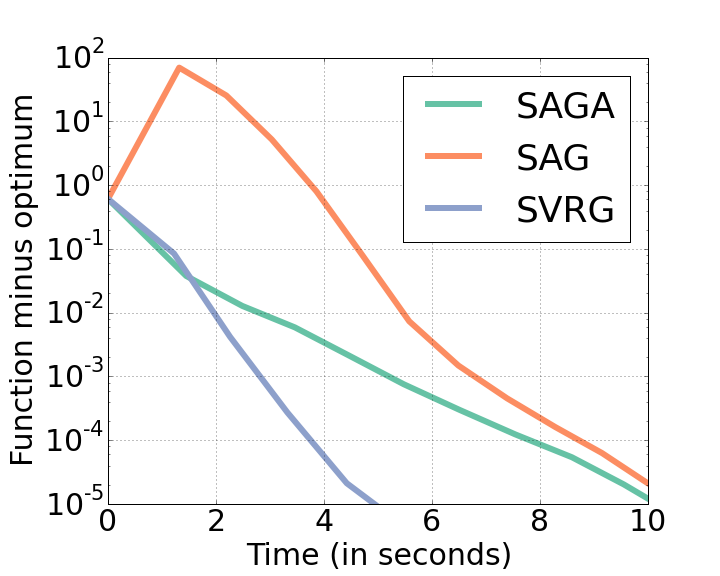
A note about the benchmarks: it is difficult to compare fairly stochastic gradient methods because at the end it usually boils down to how you choose the step size. In this plot I set the step size of all methods to 1/(3L) , where L is the Lipschitz constant of the objective function, as I think this is a popular choice. I would have prefered 1/L but SVRG was not converging for this step size. The code for the benchmarks can be found here.
-
A. Defazio, F. Bach & S. Lacoste-Julien. "SAGA: A Fast Incremental Gradient Method With Support for Non-Strongly Convex Composite Objectives" (2014). ↩
-
Rie Johnson and Tong Zhang. "Accelerating stochastic gradient descent using predictive variance reduction." Advances in Neural Information Processing Systems. 2013. ↩
-
Mark Schmidt, Nicolas Le Roux, and Francis Bach. "Minimizing finite sums with the stochastic average gradient." arXiv preprint arXiv:1309.2388 (2013). ↩↩