Due to lack of time and interest, I'm no longer maintaining this project. Feel free to grab the sources from https://github.com/fabianp/nbgallery and fork the project.

TL;DR I created a gallery for IPython/Jupyter notebooks. Check it out :-)

A couple of months ago I put online …

Last Friday was PyData Paris, in words of the organizers, ''a gathering of users and developers of data analysis tools in Python''.

The organizers did a great job in putting together and the event started already with a full room for Gael's keynote

My take-away message from the talks is …

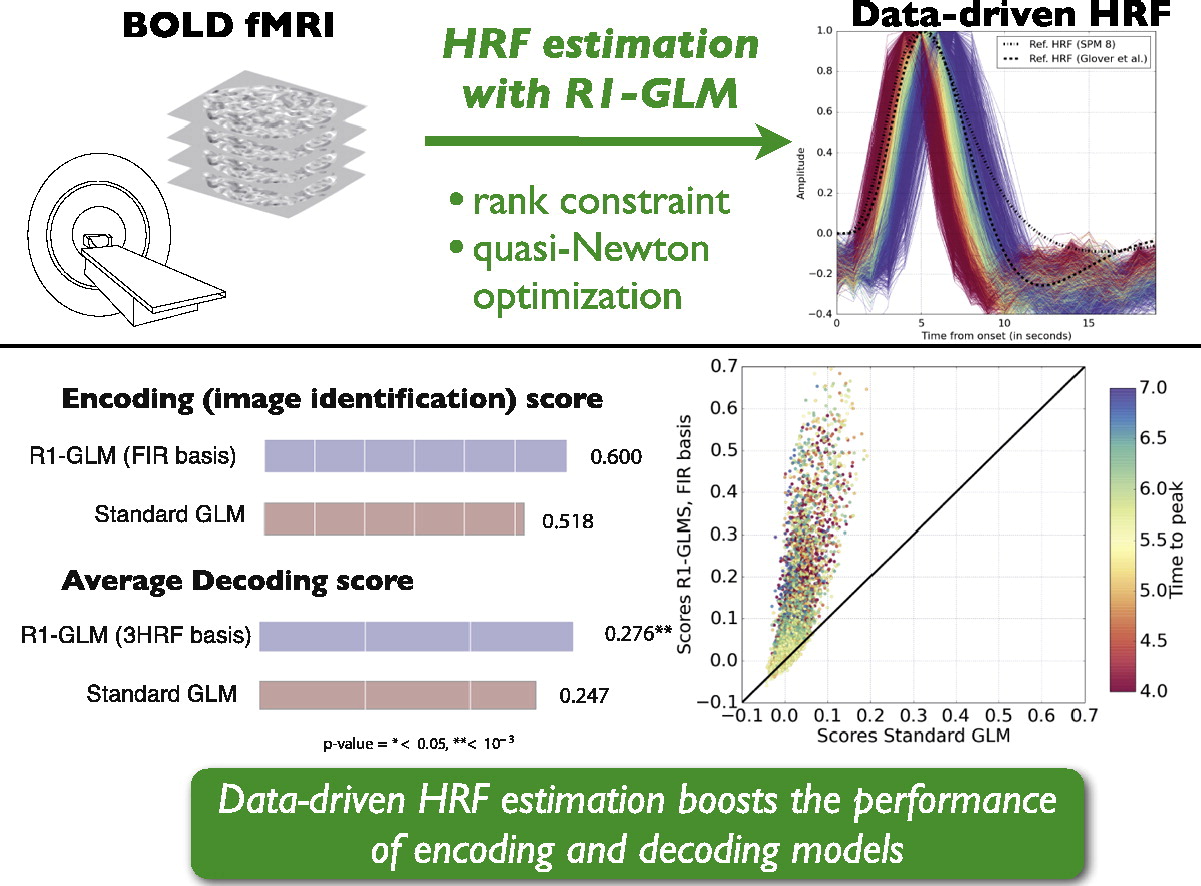
My latest research paper[¹] deals with the estimation of the hemodynamic response function (HRF) from fMRI data.

This is an important topic since the knowledge of a hemodynamic response function is what makes it possible to extract the brain activation maps that are used in most of the impressive …

:og_image: http://fa.bianp.net/blog/images/2014/mprof_example.png

One of the lesser known features of the memory_profiler package is its ability to plot memory consumption as a function of time. This was implemented by my friend Philippe Gervais, previously a colleague at INRIA and now at Google.

With …

TL; DR These are some notes on calibration of surrogate loss functions in the context of machine learning. But mostly it is …

As part of the development of memory_profiler I've tried several ways to get memory usage of a program from within Python. In this post I'll describe the different alternatives I've tested.

The psutil library

psutil is a python library that provides an interface for retrieving information on running processes. It …

In this post I compar several implementations of Logistic Regression. The task was to implement a Logistic Regression model using standard optimization …

TL;DR: I've implemented a logistic ordinal regression or proportional odds model. Here is the Python code

The logistic ordinal regression model …

My latest contribution for scikit-learn is an implementation of the isotonic regression model that I coded with Nelle Varoquaux and Alexandre Gramfort …

Householder matrices are square matrices of the form

$$ P = I - \beta v v^T$$

where $\beta$ is a scalar and $v$ is …

** Note: this post contains a fair amount of LaTeX, if you don't visualize the math correctly come to its original location **

In …

Besides performing a line-by-line analysis of memory consumption, memory_profiler exposes some functions that allow to retrieve the memory consumption of a function in real-time, allowing e.g. to visualize the memory consumption of a given function over time.

The function to be used is memory_usage. The first argument specifies what …

SciPy contains two methods to compute the singular value decomposition (SVD) of a matrix: scipy.linalg.svd and scipy.sparse.linalg.svds. In this post I'll compare both methods for the task of computing the full SVD of a large dense matrix.

The first method, scipy.linalg.svd, is perhaps …

This tutorial introduces the concept of pairwise preference used in most ranking problems. I'll use scikit-learn and for learning and matplotlib for …

My newest project is a Python library for monitoring memory consumption of arbitrary process, and one of its most useful features is the line-by-line analysis of memory usage for Python code. I wrote a basic prototype six months ago after being surprised by the lack of related tools. I wanted …

A little experiment to see what low rank approximation looks like. These are the best rank-k approximations (in the Frobenius norm) to the a natural image for increasing values of k and an original image of rank 512.

Python code can be found here. GIF animation made using ImageMagic's convert …

In scipy's development version there's a new function closely related to the QR-decomposition of a matrix and to the least-squares solution of a linear system. What this function does is to compute the QR-decomposition of a matrix and then multiply the resulting orthogonal factor by another arbitrary matrix. In pseudocode …

Last week we released a new version of scikit-learn. The Changelog is particularly impressive, yet personally this release is important for other reasons. This will probably be my last release as a paid engineer. I'm starting a PhD next month, and although I plan to continue contributing to the project …

I've been working lately in improving the scikit-learn example gallery to show also a small thumbnail of the plotted result. Here is what the gallery looks like now:

And the real thing should be already displayed in the development-documentation. The next thing is to add a static image to those …

Today's coding sprint was a bit more crowded, with some notable scipy hackers such as Ralph Gommers, Stefan van der Walt, David Cournapeau or Fernando Perez from Ipython joining in. On what got done: - We merged Jake's new BallTree code. This is a pure Cython implementation of a nearest-neighbor …

As a warm-up for the upcoming EuroScipy-conference, some of the scikit-learn developers decided to gather and work together for a couple of days. Today was the first day and there was only a handfull of us, as the real kickoff is expected tomorrow. Some interesting coding happened, although most of …

Ridge coefficients for multiple values of the regularization parameter can be elegantly computed by updating the thin SVD decomposition of the design matrix:

import numpy as np
from scipy import linalg
def ridge(A, b, alphas):
    """
    Return coefficients for regularized least squares

         min ||A x - b||^2 + alpha ||x||^2 …

I haven't worked in the manifold module since last time, yet thanks to Jake VanderPlas there are some cool features I can talk about. First of, the ARPACK backend is finally working and gives factor one speedup over the lobcpg + PyAMG approach. The key is to use ARPACK's shift-invert mode …

The manifold module in scikit-learn is slowly progressing: the locally linear embedding implementation was finally merged along with some documentation. At about the same time but in a different timezone, Jake VanderPlas began coding other manifold learning methods and back in Paris Olivier Grisel made my digits example a lot …

I decided to test my new Locally Linear Embedding (LLE) implementation against a real dataset. At first I didn't think this would turn out very well, since LLE seems to be somewhat fragile, yielding largely different results for small differences in parameters such as number of neighbors or tolerance, but …